Artigos Originais
Determinação dos parâmetros da equação de Antoine para o Metano e o Álcool Isopropílico utilizando a Evolução Diferencial
Determination of Antoine Equation Parameters for Methane and Isopropyl Alcohol using Differential Evolution
Determinación de los parámetros de la ecuación de Antoine para el Metano y el Alcohol Isopropílico mediante la Evolución Diferencial
Determinação dos parâmetros da equação de Antoine para o Metano e o Álcool Isopropílico utilizando a Evolução Diferencial
Vértices (Campos dos Goitacazes), vol. 24, núm. 1, 2022
Instituto Federal de Educação, Ciência e Tecnologia Fluminense

Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.
Recepción: 06 Agosto 2021
Aprobación: 28 Enero 2022
Resumo: A Evolução Diferencial é um método de otimização, da classe dos Algoritmos Evolucionários, inspirado em princípios da evolução biológica e utiliza-se dos operadores de mutação, cruzamento e seleção dos indivíduos de uma mesma população para realizar a busca pela solução ótima. Alguns modelos termodinâmicos, como a equação de Antoine, relacionam a pressão de vapor saturado com a temperatura através de uma relação matemática analítica. Neste artigo, foi utilizado o algoritmo da Evolução Diferencial na determinação dos coeficientes da equação de Antoine para o Metano e o Álcool Isopropílico a fim de serem comparados com os parâmetros encontrados na literatura. Para tal, foram utilizados dados experimentais disponíveis no Dortmund Data Bank. Foi observado que as previsões de pressão calculadas utilizando os parâmetros obtidos pela Evolução Diferencial apresentaram maior concordância com os dados experimentais quando comparadas com as previsões obtidas através dos parâmetros consultados na literatura.
Palavras-chave: Modelo Termodinâmico, Problemas Inversos, Inferência Estatística, Otimização.
Abstract: Differential Evolution is an optimization method, from the class of Evolutionary Algorithms, inspired by the principles of biological evolution and it uses the operators of mutation, crossover, and selection of individuals from the same population to carry out the search for the optimal solution. Some thermodynamic models such as the Antoine equation relate saturated vapor pressure to temperature through an analytical mathematical relationship. In this article, the Differential Evolution algorithm was used to determine the coefficients of the Antoine equation for Methane and Isopropyl Alcohol in order to be compared with the parameters found in the literature. For this purpose, experimental data available from the Dortmund Data Bank were used. It was observed that the pressure predictions calculated using the parameters obtained by the Differential Evolution presented a greater agreement with the experimental data when compared with the predictions obtained through the parameters consulted in the literature.
Keywords: Thermodynamic Model, Inverse Problems, Statistical Inference, Optimization.
Resumen: La Evolución Diferencial es un método de optimización, de la clase de Algoritmos Evolutivos, inspirado en los principios de la evolución biológica y utiliza los operadores de mutación, cruzamiento y selección de individuos de una misma población para llevar a cabo la búsqueda de la solución óptima. Algunos modelos termodinámicos, como la ecuación de Antoine, relacionan la presión de vapor saturado con la temperatura a través de una relación matemática analítica. En este artículo se utilizó el algoritmo Evolución Diferencial para determinar los coeficientes de la ecuación de Antoine para el metano y el alcohol isopropílico con el fin de compararlos con los parámetros encontrados en la literatura. Para ello, se utilizaron los datos experimentales disponibles del Dortmund Data Bank. Se observó que las predicciones de presión calculadas utilizando los parámetros obtenidos por el Evolución Diferencial presentaron mayor concordancia con los datos experimentales cuando se compararon con las predicciones obtenidas mediante los parámetros consultados en la literatura.
Palabras clave: Modelo termodinámico, Problemas Inversos, Inferencia Estadística, Mejoramiento.
1 Introdução
Os Algoritmos Evolucionários (AEs) são métodos de otimização que podem ser facilmente utilizados em problemas cujo comportamento da função em todo o domínio é, a priori, desconhecido ou de difícil análise. Os AEs são inspirados na evolução biológica e utilizam de um conjunto de vetores ou de indivíduos para encontrar a solução ótima (DAS; SUGANTHAN, 2011, p. 4). Cada indivíduo dessa população é uma solução em potencial e, após uma série de avaliações dos indivíduos na função objetivo, espera-se que a solução ótima do problema seja encontrada.
Dentre os AEs pode-se destacar o algoritmo da Evolução Diferencial (ED), que é um método estocástico de otimização em que a solução ótima é encontrada através da mutação, cruzamento e seleção dos indivíduos de uma população. Esse método tem se tornado popular nos últimos anos devido a sua boa convergência, fácil implementação e amplo uso em problemas em que a função é não diferenciável, multimodal ou complexa (KARABOĞA; ÖKDEM, 2004, p. 54).
Uma das possíveis aplicações da ED é na otimização de modelos termodinâmicos que representam fenômenos que envolvem calor e outras formas de energia. A equação de Antoine é uma entre as várias equações existentes que relacionam a pressão de vapor saturado com a temperatura e ela descreve o comportamento de sistemas em que a pressão exercida pela fase vapor de uma substância, em um recipiente fechado, está em equilíbrio termodinâmico com o líquido gerador (RODGERS; HILL, 1978, p. 415; THOMSON, 1946, p. 10). A Equação de Antoine se destaca tanto pela sua simplicidade quanto sua precisão, e seus parâmetros podem ser estimados através do método de máxima verossimilhança ao se utilizar dados experimentais conhecidos (DE LA CALLE-ARROYO; LÓPEZ-FIDALGO; RODRÍGUEZ-ARAGÓN, 2021).
Durante o processo de formulação de um modelo matemático para representação de um determinado fenômeno, surgem alguns parâmetros que não podem ou são difíceis de serem medidos. O valor dessas grandezas pode ser inferido a partir de um conjunto de observações utilizando para tal um procedimento denominado de Problema Inverso. Os valores desses parâmetros são ajustados pela comparação com dados experimentais confiáveis, de forma que possam ser utilizados para simular o comportamento do sistema para diferentes condições de operação. Evita-se, assim, a necessidade da realização de experimentos específicos para uma dada condição (LOBATO; STEFFEN JUNIOR, 2008; SCHWAAB; PINTO, 2007).
No presente estudo, foi aplicado o algoritmo da Evolução Diferencial na identificação de parâmetros presentes na equação de Antoine para o Metano e o Álcool Isopropílico. O problema inverso é formulado considerando o procedimento da máxima verossimilhança resultando num problema de otimização no qual a função objetivo deve ser minimizada. Os dados experimentais de pressão de vapor saturado, de temperatura e as constantes de Antoine, utilizados neste trabalho, foram retirados do DORTMUND DATA BANK (2021).
2 Metodologia
A pressão de vapor saturado é uma medida da volatilidade que ocorre nas fases líquido-vapor de uma substância presente em um recipiente fechado. Em síntese, considerando um recipiente fechado, submetido a tal pressão de vapor, é possível afirmar que uma quantidade de moléculas da fase líquida da substância vai evaporar enquanto uma parte das moléculas da fase vapor da substância vão condensar. Quando a taxa com que as moléculas da fase líquida evaporam for igual a taxa com que as moléculas da fase vapor condensam, é dito que o sistema está em um equilíbrio termodinâmico. Para aumentar a taxa com que as moléculas evaporam, é necessário aumentar a temperatura do sistema que, consequentemente, irá aumentar a pressão no recipiente e causará um aumento na taxa com que as moléculas condensam (JESPERSEN, 2014).
A pressão de vapor saturado depende diretamente da natureza da substância e da temperatura do sistema. O modelo mais recomendado para uso geral que relaciona a pressão de vapor saturado com a temperatura é a equação de Antoine que foi proposta inicialmente em 1888 pelo engenheiro francês Louis Charles Antoine (THOMSON, 1946, p. 1). A partir da equação de Clausius-Clapeyron, é gerada a Equação de Antoine (Equação 1), que é uma função semiempírica obtida através de correlações empíricas com resultados de ensaios experimentais (RODGERS; HILL, 1978, p. 415):
onde os parâmetros A, B e C são obtidos de dados experimentais e se comportam de acordo com a substância e com a temperatura do sistema.
Geralmente, para uma mesma substância, são utilizados dois conjuntos de constantes, um conjunto que vai do ponto triplo ao ponto de ebulição e outro conjunto que vai do ponto de ebulição ao ponto crítico. As unidades da Equação 1 dependem dos coeficientes, mas na maioria dos casos, os valores de pressão (P) e de temperatura (T) são dados, respectivamente, em milímetros de mercúrio e em Kelvin.
A estimação de parâmetros através da técnica de problemas inversos consiste na minimização de uma função objetivo que compara a resposta obtida pela solução do problema direto com a resposta observada pelos dados experimentais. Para isso, a partir de uma dada métrica, formula-se o problema de tal maneira que se possa estimar um conjunto de parâmetros que melhor se ajustam ao conjunto de valores medidos de entrada e saída (SILVA NETO; BECCENERI, 2012). Geralmente, problemas inversos têm sido resolvidos através de técnicas de otimização determinísticas. Por outro lado, devido a sua simplicidade, muitos trabalhos propõem a utilização de técnicas de otimização estocásticas que podem ser acopladas ou não aos métodos determinísticos (OLIVEIRA et al., 2018).
Quanto à natureza de solução, os problemas inversos podem ser aplicados para estimativa de parâmetros ou de funções. Neste trabalho, o problema inverso da equação de Antoine consiste em encontrar os parâmetros A, B e C que melhor se ajustam a um conjunto de dados experimentais. Diferentes fatores contribuem para as incertezas na identificação desses parâmetros, entre eles, podem-se citar os erros de medição presentes nas observações experimentais. Uma das técnicas estocásticas que consideram essas incertezas é a máxima verossimilhança cujo procedimento resulta num problema de otimização no qual a função objetivo, que quantifica os desvios entre as previsões de um modelo e suas observações experimentais, deve ser minimizada. Considerando que esses erros experimentais são cumulativos, não correlacionados, e podem ser modelados pela distribuição normal, com média zero e desvio padrão constante, então a função objetivo a ser minimizada para obtenção de estimativas de máxima verossimilhança pode ser representada pelo somatório dos resíduos quadrados entre as observações experimentais e as respostas do modelo (SCHWAAB; PINTO, 2007, p. 252), conforme Equação 2:
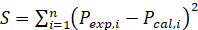 (2)
(2)em que Pexp é o vetor com as pressões experimentais, Pcal é o vetor que contém as pressões calculadas através da Equação 1 e n é o número total de medidas experimentais.
Na próxima seção são apresentados os fundamentos teóricos para a solução do problema inverso de acordo com a abordagem estocástica do método da Evolução Diferencial (ED) para estimação de parâmetros presentes na Equação 1.
2.1 Evolução Diferencial
Dentre as inúmeras técnicas estocásticas de busca e identificação de parâmetros destaca-se o algoritmo da ED que foi proposto em 1995 por Storn e Price e realiza a otimização através de uma busca paralela e direta (STORN; PRICE, 1995, p. 5). Inicialmente, são especificados os parâmetros do algoritmo, sendo que, na versão clássica, são utilizadas apenas três variáveis: a probabilidade de cruzamento CR, o tamanho da população Np e a taxa de perturbação F (STORN; PRICE, 1997, p. 345). Nesta etapa também podem ser especificados o número máximo de gerações (G) e os limites inferiores (LINF) e superiores (LSUP) de cada parâmetro do problema. Depois de serem definidas as variáveis do algoritmo é inicializada uma população de Np indivíduos aleatórios (Equação 3).
em que é o i-ésimo indivíduo da população, conhecido como indivíduo alvo, e são, respectivamente, os vetores com os limites superiores e inferiores, randj (0,1) é um número aleatório gerado entre 0 e 1 e j = 1, 2, 3, …, D, sendo D o número de dimensões do problema.
Após a população inicial ser criada, para cada indivíduo da população, são gerados novos vetores através do operador de mutação, utilizando a soma da diferença ponderada entre dois vetores a um terceiro como mostrado na expressão seguinte (Equação 4).
onde é o vetor criado na mutação, conhecido como indivíduo doador, , e são indivíduos diferentes entre si e do indivíduo atual da população, escolhidos aleatoriamente, e F ∈ [0,2].
Note que, quando os vetores estiverem se aproximando da solução ótima, a diferença ponderada presente na Equação 4 irá diminuir automaticamente. Assim, o intervalo de busca de cada parâmetro irá ser ajustado de acordo com os indivíduos (GÄMPERLE; MÜLLER; KOUMOUTSAKOS, 2002, p. 2).
Com o operador de cruzamento, são gerados novos indivíduos, chamados de experimentais, a partir do cruzamento dos indivíduos doadores e dos indivíduos alvos. Para tal, é gerado um número aleatório Y para cada dimensão do problema. Se este número for menor ou igual a CR, o indivíduo experimental herda o valor da componente j do vetor doador. Caso contrário, ele herda o valor do vetor alvo. O modelo matemático deste operador é dado na Equação 5.
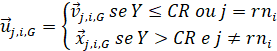 (5)
(5)em que Y ∈ [0,1], rni é um índice escolhido aleatoriamente em [1, D] para cada indivíduo da população e CR ∈ [0,1]. A igualdade j = rni certifica que o indivíduo experimental receberá pelo menos um cromossomo do indivíduo doador.
Após a mutação e o cruzamento, os indivíduos experimentais e os alvos são avaliados na função objetivo. Se o problema for de minimização e o indivíduo experimental apresentar um resultado menor na função objetivo, ele substitui o indivíduo alvo na população e é utilizado na próxima geração. Na Equação 6, é mostrado o operador de seleção:
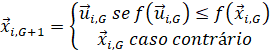 (6)
(6)onde é o i-ésimo indivíduo experimental, é i-ésimo indivíduo alvo e G é a geração atual.
A Equação 6 garante que apenas os melhores indivíduos serão utilizados nas futuras gerações. Em seguida, o algoritmo avança uma geração e repete os operadores de mutação, cruzamento e seleção até que o critério de parada seja satisfeito.
As definições dos operadores mencionados anteriormente fazem parte da versão conhecida como DE/rand/1/bin do algoritmo da evolução diferencial. Cada versão do algoritmo pode ser escrita no formato DE/x/y/z, sendo que x especifica a estratégia utilizada na mutação, y é o número de operações de diferença vetorial empregados e z indica qual o tipo de cruzamento (STORN; PRICE, 1997, p. 346). Neste estudo foi utilizada a versão DE/rand/1/bin considerando como critério de parada o número máximo de gerações. O seu algoritmo é apresentado a seguir:
Passo 1. Entrada das variáveis G, CR, F, Np, e do espaço de busca dos parâmetros do problema;
Passo 2. Gerar a população inicial;
Passo 3. Repetir os passos 4 ao 9 até G gerações;
Passo 4. Repetir os passos 5 ao 9 até o tamanho total da população;
Passo 5. Escolher aleatoriamente os vetores , e e ;
Passo 6. Repetir os passos 7 ao 9 até D dimensões;
Passo 7. Gerar aleatoriamente o valor Y;
Passo 8. Aplicar a Equação (4) para encontrar os componentes do vetor
Passo 9. Avaliar os vetores e na função objetivo;
Passo 10. Retornar o melhor indivíduo e o valor da função objetivo correspondente.
2.2 Dados Experimentais
O comportamento do processo dos métodos estocásticos está relacionado com as informações experimentais existentes, ou seja, a qualidade da solução do problema inverso depende diretamente da qualidade dos dados experimentais selecionados. Neste trabalho, para minimizar a função objetivo presente na Equação 2, foi utilizado o algoritmo da Evolução Diferencial e foram usados dados experimentais de pressão de vapor saturado disponíveis no Dortmund Data Bank (DDB). Para o metano, foram utilizados 68 valores de pressão e temperatura com T ∈ [-160,8; -83,05] °C e para o Álcool Isopropílico foram utilizados 66 dados experimentais com T ∈ [85,09; 202,36] °C (DORTMUND DATA BANK, 2021).
Com o objetivo de verificar a qualidade dos resultados obtidos pela ED, os dados experimentais de cada substância foram divididos em dois grupos: um grupo de determinação dos parâmetros e outro de validação, sendo os dados escolhidos aleatoriamente dentro do conjunto total de dados disponíveis. O primeiro conjunto foi utilizado na regressão da equação de Antoine a fim de se determinar as constantes A, B e C de cada substância. O segundo grupo, de validação, foi utilizado para verificar a qualidade dos resultados encontrados pelo algoritmo da ED através de uma análise gráfica e numérica. Para o Metano, cada conjunto teve 34 dados, enquanto no Álcool Isopropílico, cada conjunto teve 33 dados.
3 Resultados
Para determinar os parâmetros presentes na equação de Antoine das substâncias foram utilizados os seguintes valores: Np = 50, F = 0,8, CR = 0,85 e G = 600. Para o intervalo do espaço de busca foram utilizados como referência os coeficientes de Antoine disponíveis no DDB (DORTMUND DATA BANK, 2021). Assim, o intervalo de cada constante empregado no algoritmo foi: A ∈ [1, 50] mmHg, B ∈ [50, 5000] ºC e C ∈ [50, 5000] ºC.
Na Tabela 1 são apresentados os resultados encontrados para as duas substâncias com as constantes da literatura (DDB) e com as constantes obtidas neste trabalho (DE/rand/1/bin). Na quinta coluna da Tabela 1 são apresentados os valores mínimos para a função objetivo dada pela Equação 2, empregando o conjunto de dados de validação, após a obtenção das constantes A, B e C empregando os dados experimentais para ajuste da curva. Na penúltima coluna, são mostrados os erros relativos médios percentuais entre as pressões calculadas e as pressões do conjunto de validação.
| Substância | A(mmHg) | B(ºC) | C(ºC) | MIN (x106)(mmHg2) | Erro (%) | Referência |
| Álcool Isopropílico | 7,9584 | 1519,66 | 216,829 | 4,467505 | 2,7935 | DDB |
| 7,6719 | 1383,77 | 208,795 | 0, 517351 | 1,8350 | DE/rand/1/bin | |
| Metano | 6,7021 | 394,48 | 264,609 | 5, 469397 | 2,6493 | DDB |
| 7,0121 | 490,15 | 280,500 | 3, 668051 | 1,6545 | DE/rand/1/bin |
Da Tabela 1, nota-se que os valores mínimos obtidos na função objetivo foram menores com os coeficientes encontrados pelo algoritmo. Consequentemente, o erro relativo médio percentual também foi menor. Assim, as pressões calculadas com os coeficientes encontrados pelo algoritmo aproximaram-se melhor do conjunto de dados do grupo de validação.
Nas Figuras 1 e 2 são mostradas as curvas com as pressões do conjunto de validação das respectivas substâncias e as curvas das pressões calculadas com os parâmetros encontrados (DE/rand/1/bin) e com as constantes disponíveis na literatura. Os gráficos ilustram a boa qualidade do ajuste em comparação com os dados experimentais (DORTMUND DATA BANK, 2021).
Nas Figuras 3 e 4 são mostrados os erros relativos percentuais em módulo entre as pressões calculadas e as experimentais do conjunto de validação. Pode-se observar a boa concordância entre os valores, apresentando um erro relativo percentual na ordem de 8%, o que era esperado, demonstrando que é razoável a aderência entre as curvas experimentais e teóricas.
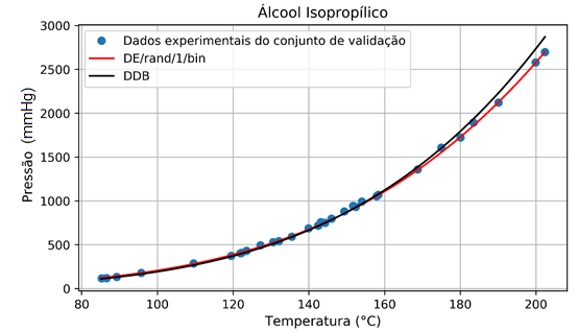
Figura 1.
Pressões experimentais e as calculadas pela equação de Antoine para o conjunto de validação do Álcool Isopropílico
Fonte: Os autores
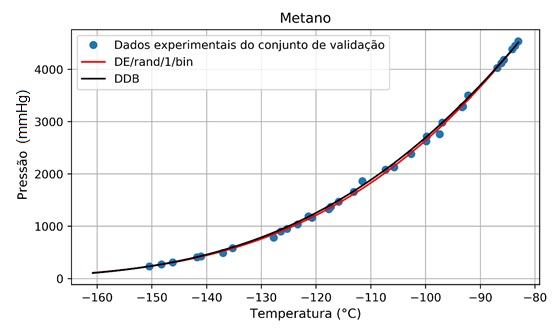
Figura 2.
Pressões experimentais e as calculadas pela equação de Antoine para o conjunto de validação do Metano
Fonte: Os autores
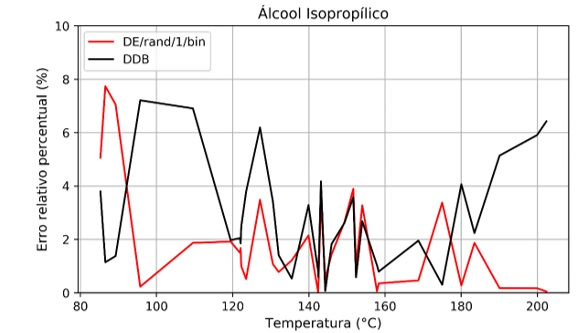
Figura 3.
Erro relativo percentual entre as pressões experimentais e as calculadas pela equação de Antoine para o conjunto de validação do Álcool Isopropílico
Fonte: Os autores
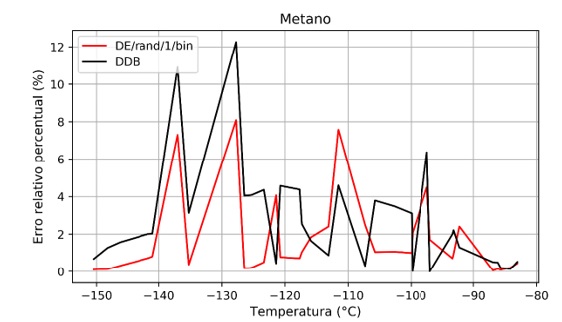
Figura 4.
Erro relativo percentual entre as pressões experimentais e as calculadas pela equação de Antoine para o conjunto de validação do Metano
Fonte: Os autores
As Figuras 3 e 4 mostram que, embora em determinados pontos, as pressões obtidas com os coeficientes encontradas pelo algoritmo resultaram em erros relativos percentuais maiores, é possível afirmar que o erro relativo médio percentual foi reduzido ao se comparar as pressões calculadas com os parâmetros deste trabalho e aqueles encontrados na literatura.
4 Considerações finais
A metodologia aqui apresentada foi detalhadamente desenvolvida para a reprodução de comportamentos físicos esperados, permitindo construir perfis de evolução de pressões de vapor saturado para diferentes tipos de substâncias.
Os resultados, empregando-se a abordagem estocástica por meio do método de Evolução Diferencial (ED), demonstraram eficácia significativa para resolver o problema de identificação de parâmetros presentes na equação de Antoine, que modela a relação entre a temperatura e a pressão de vapor saturado. Por meio das análises gráficas e numéricas das pressões, foi possível constatar que os coeficientes encontrados pelo algoritmo da ED apresentaram maior concordância com os dados experimentais ao serem aplicados à equação de Antoine quando confrontados com os coeficientes disponibilizados na literatura. Como consequência da boa convergência das pressões, resultantes da boa determinação das constantes, houve uma diminuição do erro relativo médio percentual entre as previsões das pressões calculadas com as constantes da literatura e das constantes encontradas neste trabalho.
Para trabalhos futuros especula-se fazer a análise de novas substâncias, com o emprego da Evolução Diferencial ou de outras técnicas estocásticas de otimização como o algoritmo de colisão de partículas e inferência bayesiana através do método de Monte Carlo com Cadeias de Markov (KAIPIO; SOMERSALO, 2006; KALOS; WHITLOCK, 2009). Sugere-se também a utilização de métodos híbridos, ou seja, métodos estocásticos em conjunto com métodos determinísticos de otimização, o que possibilita a redução do custo computacional e consequentemente um maior número de execuções do processo iterativo, simulando-se diferentes conjuntos de dados experimentais para diferentes substâncias.
Referências
DAS, S.; SUGANTHAN, P. N. Differential evolution: a survey of the state-of-the-art. IEEE transactions on evolutionary computation, v. 15, n. 1, p. 4-31, 2011. DOI: https://doi.org/10.1109/TEVC.2010.2059031.
DE LA CALLE-ARROYO, C.; LÓPEZ-FIDALGO, J.; RODRÍGUEZ-ARAGÓN, L. J. Optimal designs for Antoine Equation. Chemometrics and Intelligent Laboratory Systems, v. 214, p. 104334, 2021. DOI: https://doi.org/10.1016/j.chemolab.2021.104334.
DORTMUND DATA BANK. Thermophysical properties of pure component and mixtures. 2021. Disponível em: http://www.ddbst.com. Acesso em: 20 jul. 2021.
GÄMPERLE, R.; MÜLLER, S. D.; KOUMOUTSAKOS, P. A parameter study for differential evolution. Advances in intelligent systems, fuzzy systems, evolutionary computation, v. 10, n. 10, p. 293-298, 2002.
JESPERSEN, N. D. Barron's AP Chemistry. 7. ed. New York: Barron’s Educational Series, 2014.
KAIPIO, J.; SOMERSALO, E. Statistical and computational inverse problems. New York: Springer Science & Business Media, 2006.
KALOS, M. H.; WHITLOCK, P. A. Monte Carlo methods. New York: John Wiley & Sons, 2009.
KARABOĞA, D.; ÖKDEM, S. A simple and global optimization algorithm for engineering problems: differential evolution algorithm. Turkish Journal of Electrical Engineering & Computer Sciences, v. 12, n. 1, p. 53-60, 2004.
LOBATO, F. S.; STEFFEN JR., V. Algoritmo de Luus-Jaakola aplicado a um problema inverso de fermentação batelada alimentada. Trends in Computational and Applied Mathematics, v. 9, n. 3, p. 417-426, 2008.
OLIVEIRA, C. et al. Estimation of kinetic parameters in a chromatographic separation model via Bayesian inference. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, v. 34, n. 1, 2018. DOI: http://dx.doi.org/10.23967/j.rimni.2017.12.002.
RODGERS, R. C.; HILL, G. E. Equations for vapour pressure versus temperature: derivation and use of the Antoine equation on a hand-held programmable calculator. British Journal of Anaesthesia, v. 50, n. 5, p. 415-424, 1978. DOI: https://doi.org/10.1093/bja/50.5.415.
SCHWAAB, M.; PINTO, J. C. Análise de Dados Experimentais: I. Fundamentos de Estatística e Estimação de Parâmetros. São Paulo: Editora E-papers, 2007.
SILVA NETO, A. J.; BECCENERI, J. C. Técnicas de inteligência computacional inspiradas na natureza, aplicação em problemas inversos de transferência radiativa, notas em matemática aplicada. Sociedade Brasileira de Matemática Aplicada e Computacional, São Carlos, SP, v. 41, 2012.
STORN, R.; PRICE, K. Differential evolution-A simple and efficient adaptive scheme for global optimization over continuous spaces [R]. Berkeley: ICSI, 1995.
STORN, R.; PRICE, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization, v. 11, n. 4, p. 341-359, 1997.
THOMSON, G. W. The Antoine equation for vapor-pressure data. Chemical reviews, v. 38, n. 1, p. 1-39, 1946. DOI: https://doi.org/10.1021/cr60119a001.
Notas de autor
Información adicional
COMO CITAR (ABNT): SOUZA, A. L. R. et al. Determinação dos parâmetros da equação de Antoine para o Metano e o Álcool Isopropílico utilizando a Evolução Diferencial. Vértices (Campos dos Goitacazes), v. 24, n. 1, p. 168-180, 2022. DOI: https://doi.org/10.19180/1809-2667.v24n12022p168-180. Disponível em: https://www.essentiaeditora.iff.edu.br/index.php/vertices/article/view/16284.
COMO CITAR (APA): Souza, A. L. R., Ribeiro, D. G., Grigorio, L. S., Muniz, V. S. B. & Martins, I. M. (2022). Determinação dos parâmetros da equação de Antoine para o Metano e o Álcool Isopropílico utilizando a Evolução Diferencial. Vértices (Campos dos Goitacazes), 24(1), 168-180. https://doi.org/10.19180/1809-2667.v24n12022p168-180.
