1 Introdução

A Mecânica Quântica (MQ) representa um dos principais modelos teóricos para a explicação da realidade física, especialmente nos aspectos relativos à estrutura íntima da matéria (BOHR, 1995; PESSOA JUNIOR, 2000). Sem embargo, a influência da teoria não se restringe ao âmbito da física, podendo-se divisar inúmeras conseqüências filosóficas, dentre as quais as questões (1) da realidade do mundo subatômico — esfera ontológica — e (2) da possibilidade de se conhecê-la — esfera epistemológica (SIQUEIRA-BATISTA et al., 2003).

Um dos pontos chaves neste último domínio — esfera epistemológica — é a indeterminação das descrições da MQ (HEISENBERG, 1958). Neste sentido, quando são conduzidas certas experiências utilizando-se os princípios teóricos da MQ, torna-se impossível obter uma descrição completa dos fenômenos — ou seja, estes experimentos têm um alcance limitado por algumas particularidades. Como exemplo, pode-se citar o comportamento dos elétrons, que ora se manifestam como se fossem possuidores de uma “natureza ondulatória”, ora como se detentores de uma “natureza corpuscular”.

Além disso, não é possível obter em um único experimento uma informação referente à posição e ao momentum de uma dessas partículas, ou seja, em qualquer medida feita sempre haverá uma incerteza, caracterizando o célebre Princípio da Incerteza de Heisenberg (CHIBENI, 2005), expresso nos seguintes termos:

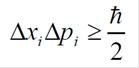
e

onde

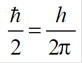
sendo h a constante de Planck; Δx_i, Δp_i, Δt e ΔE designam, respectivamente, as incertezas nas coordenadas de posição, nas componentes do momento, no tempo e na energia.

A visão instaurada pela MQ trouxe especiais problemas às tradições de pesquisa que se ancoravam na investigação das leis deterministas do mundo objetivo — ou seja, referida aos processos físicos que têm lugar no espaço e no tempo, como na esclarecedora citação de Laplace: “[...] toda a história do Universo poderia ser conhecida se a posição e a velocidade de uma partícula fossem conhecidas em qualquer instante do tempo” (LAPLACE, 1884).

Tal aspecto — considerado paradoxal para a imagem de mundo vigente — concorreu para que a MQ fosse questionada em sua completude, âmago da célebre polêmica de Einstein e Bohr. De fato, se para Bohr — e demais cientistas da Escola de Copenhague —, a MQ era uma teoria completa em sua proposta de descrição do mundo atômico — ou seja, não haveria como se libertar da incerteza dessas medidas (BOHR, 1995) —, para Einstein, a MQ não passaria de um modelo incompleto, considerando que novas variáveis ocultas seriam inseridas na modelação matemática quântica, permitindo refutar o princípio da incerteza (neste princípio estava, segundo sua percepção, a “falha” da teoria quântica) — afinal, “Deus não joga dados” (EINSTEIN, 1953).

É neste contexto polêmico que se inscreve a interpretação de Bohm para a MQ — em termos de —, na qual se prevê uma “descrição causal e objetiva para os fenômenos quânticos” (FREIRE JUNIOR et al., 1994). Discutir tal proposta é o escopo do presente artigo.

2 A mecânica bohmiana

O ponto de partida para a teoria de Bohm foi a não aceitação das interpretações “clássicas” da MQ, no que se refere às variáveis ocultas, como concebido pela Escola de Copenhague. A interpretação bohmiana da MQ não-relativista envolve as variáveis ocultas, baseada na existência de partículas descrevendo trajetórias no espaço segundo uma lei de movimento que pode ser obtida a partir da função de onda (BOHM, 1957).

Deste modo, já em 1952, Bohm foi capaz de demonstrar explicitamente que parâmetros poderiam ser introduzidos na mecânica ondulatória não-relativista, tornando a descrição indeterminista em uma determinista (BOHM, 1952A; BOHM, 1952B).

Na proposta bohmiana para a teoria quântica, atribui-se uma ontologia aos sistemas físicos. No caso particular da mecânica quântica não-relativista, os sistemas físicos são compostos por partículas puntiformes que se movem descrevendo trajetórias quânticas no espaço, como uma lei de evolução atribuída às partículas de acordo com a prescrição:

(1)

onde o ponto sobre o vetor-posição representa a operação de derivada temporal e S parametriza a função de onda, Ψ, de acordo com a decomposição polar

(2)

e m é a massa inercial da partícula. Esta função de onda, da mesma forma que na interpretação de Copenhague, satisfaz à equação de Schröndinger

(3)

onde V representa o potencial clássico.

Com a decomposição polar, acima, para Ψ introduzida na equação (2), é possível chegar-se às equações a seguir para R e S:

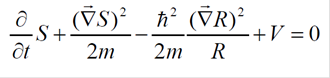(4)

e

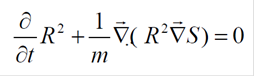(5)

Um passo crucial que marca a singularidade da formulação de Bohm consiste em encarar a equação (4)como uma equação clássica de Hamilton-Jacobi:

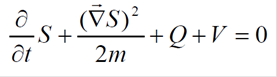(6)

onde

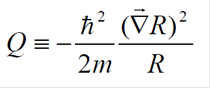(7)

é interpretado como um potencial quântico, ao lado do potencial clássico, V. O caráter quântico de Q fica assinalado pela presença manifesta da constante de Planck em sua expressão.

A partir da identificação da equação (6) como uma equação do tipo Hamilton-Jacobi, pode-se escrever o momento e a velocidade da partícula em termos da fase, S, respectivamente, como segue abaixo:

(8)

e

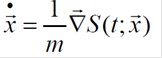(9)

Desta forma, o momento, p(t;x), e a x(t;x) velocidade, são determinados pelo campo de fase, S, permitindo a obtenção de uma trajetória bem definida, a qual se denomina trajetória bohmiana. Conhecendo-se, então, Ψ(t;x) como dada na equação (2), tem-se que as trajetórias podem ser univocamente determinadas pelas condições iniciais, através de um sistema acoplado de equações diferenciais de primeira ordem, em geral, não-lineares. É este aspecto que confere ao tratamento bohmiamo a característica de uma formulação determinística, na qual o princípio da incerteza de Heisenberg perde o caráter fundamental presente na interpretação probabilística usual.

É importante ressaltar que a formulação de Bohm — como desenvolvida em colaboração com Hiley e Kaloyerou (1987) — não descarta a equação de Schrödinger, mas a acopla ao conjunto de equações diferenciais de primeira ordem dado anteriormente, conduzindo, então, a um amplo conjunto de equações acopladas (BOHM; HILEY, 1999). Ademais, reescrevendo a função de onda — solução da equação de Schrödinger — estabelece-se analogia com a física clássica, demonstrando que a mecânica newtoniana encontra um tratamento análogo no mundo quântico; de fato, Bohm escreve uma espécie de segunda lei de Newton para uma partícula quântica. Trata-se, em última análise, de uma “recuperação do determinismo próprio à física clássica” (FREIRE JUNIOR et al., 1994).

Cabe ainda destacar que a equivalência entre as abordagens via equação de Schröndinger à la Copenhague e via equação de Bohm pode ser claramente ilustrada em sistemas fundamentais como o caso da partícula livre, do oscilador harmônico simples, da partícula sujeita a um poço de potencial unidimensional e da partícula carregada minimamente acoplada a um campo eletromagnético externo. Recomenda-se a consulta aos trabalhos de J. M. F. Bassalo e colaboradores (2003) e de P. R. Holland (1993) para uma apreciação mais minuciosa destes sistemas físicos.

3 Considerações finais

A interpretação de Bohm para a MQ permaneceu no ostracismo por alguns anos. Entre os possíveis motivos para tal situação estavam (1) a potencial não-localidade que decorre do emaranhamento e (2) o ressurgimento do determinismo clássico — descrição do micromundo utilizando categorias como casualidade, posição . trajetória, com um significado físico “concreto” — que a descrição em termos de variáveis ocultas apresenta (a discussão acerca deste último aspecto, a trajetória — a propósito das abordagens de Copenhague e Bohm —, será objeto de trabalho em vias de conclusão – SIQUEIRA-BATISTA et al, 2008). Entretanto, mais recentemente, tem se renovado o interesse pela mecânica bohmiana, na medida em que os debates sobre o determinismo permanecem em pauta (ALEKSANDROWICZ, 2007; ATLAN, 2003) e a propriedade de não-localidade já não é mais um problema tão grande para a física — por exemplo, as teorias de cordas (KAKU, 2000) adotadas para a descrição da matéria em sua escala mais fundamental, não são modelos locais no sentido usual do conceito.

As perspectivas para a aplicação da mecânica de Bohm, em diferentes áreas — como a teoria quântica de campos e a física de altas energias, física da matéria condensada, cosmologia quântica e teoria da informação quântica — são notáveis, cabendo, na atualidade, a condução de novas investigações em torno dos seus conceitos, teorias e métodos.

Referências

ALEXANDROWICZ, A. M. C. O paradigma da complexidade no século XXI: da filosofia e ética da biologia a uma evolução antropológica e psicoafetiva em curso. Tese. Escola Nacional de Saúde Pública Sérgio Arouca, FIOCRUZ, 2007.

ATLAN, H. Ruído e determinismo: diálogos espinosistas entre antropologia e biologia. Maná, v. 9, p. 123-137, 2003.

BASSALO, J. M. F. et. al. Tópicos da Mecânica Quântica de de Broglie-Bohm. Belém: EDUFPA, 2003.

BOHM, D.; HILEY, B. J.; KALOYEROU, P. N. An ontological basis for the Quantum Theory. Phys Rep, v. 144, p. 349, 1987.

BOHM, D.; HILEY, B. J. The undivided universe: an ontological interpretation of quantum theory. London: Routledge, 1999.

BOHM, D. A suggested interpretation of the quantum theory in terms of hidden variables. I. Phys Rev, v. 85, p.166-179, 1952a.

BOHM, D. A suggested interpretation of the quantum theory in terms of hidden variables. II. Phys Rev, v. 85, p. 180-193, 1952b.

BOHM, D. Causality and Chance in Modern Physics. Philadelphia: Routledge & Kegan Paul and D. Van Nostrand Company, 1957.

BOHR, N. Física Atômica e Conhecimento Humano. Rio de Janeiro: Contraponto, 1995.

CHIBENI, S. S. Certezas e incertezas sobre as relações de Heisenberg. Revista Brasileira de Ensino de Física, v. 27, p. 181-192, 2005.

EINSTEIN, A. Elementare Überlegungen zur interpretation der grundlagen der quanten-mechanik. Edinburgh: University of Edinburgh, 1953.

FREIRE JUNIOR, O.; PATY, M.; BARROS, A. L. R. David Bohm, sua estada no Brasil e a teoria quântica. Estud av, v. 8, p. 53-82, 1994.

HEISENBERG, W. Physics and philosophy. New York: Harper Torchbooks, 1958.

HOLLAND, P. R. The quantum theory of motion. Cambridge: Cambridge University Press, 1993.

KAKU, M. Strings, conformal fields and M-Theory. Springer: Series Graduate Texts in Contemporary Physics, 2000.

LAPLACE, P. S. Oeuvres completes. Paris: Gauthier-Villars; 1884.

PESSOA JUNIOR, O. Histórias contrafactuais: o surgimento da Física Quântica. Estudos avançados, v. 14, n. 39, p.175-204, 2000.

SIQUEIRA-BATISTA, R. et. al. A realidade quântica – notas históricas e apontamentos epistemológicos. Physicae, v. 4, p. 33-38, 2003.

SIQUEIRA-BATISTA, R. et. al. A mecânica quântica de David Bohm: implicações epistemológicas. Revista Brasileira de Ensino de Física. 2008 (submetido).

Notas de autor