1 Considerações preliminares

No presente artigo buscamos rever e sistematizar aspectos teórico-conceituais que têm servido de base para uma série de prescrições voltadas para a atividade de avaliação de desempenho escolar em Matemática. Tais contribuições vêm do campo de trabalho da Psicologia da Educação Matemática, viés este imposto pela formação do autor (para uma breve apresentação do domínio da Psicologia da Educação Matemática) (FALCÃO, 2003). Nesse sentido, o título do artigo faz um jogo de palavras alusivo a uma das obras mais conhecidas do grupo de pesquisa e formação, sediado na pós-graduação em Psicologia Cognitiva do departamento de Psicologia da Universidade Federal de Pernambuco, o livro “Na vida dez, na escola zero” (CARRAHER; SCHLIEMANN, 1988). Em tal livro, os autores fazem menção a crianças de nível sócio-econômico muito baixo e com sérios problemas de escolaridade (fracasso e evasão escolares), porém, demonstrando excelente desempenho em problemas matemáticos envolvendo adição e subtração, em contexto extra-escolar de comércio (gestão de dinheiro em situações de comércio referentes à prestação de serviços, como guarda de automóveis, e vendas de produtos variados). Um dado interessante, mostrado pelos autores supracitados, foi o baixo nível de desempenho em problemas matematicamente isomórficos àqueles problemas propostos em contexto de vida extra-escolar, quando tais problemas eram transpostos e apresentados em formato típico do contexto escolar; em outras palavras, aquelas crianças eram capazes de operar, impecavelmente, com grandezas numéricas em contexto comercial (“na vida dez...”), mas quando essas mesmas grandezas e operações eram transpostas para o contexto típico dos problemas escolares, estas mesmas crianças mostravam problemas graves de desempenho (“...na escola zero”). Dados semelhantes foram constatados, pelo mesmo grupo de pesquisa mencionado acima, quando foram estudadas as competências matemáticas de vários grupos de adultos de baixa escolarização, como cambistas de jogo de bicho de Recife (ACIOLY, 1985), trabalhadores “bóias-frias” da colheita da cana em Pernambuco (ACIOLY, 1994; ABREU, 1988), feirantes (LIMA, 1986) e carpinteiros (SCHLIEMANN, 1984). Mais recentemente, a questão das diferenças e pontos em comum entre as competências matemáticas escolares e extra-escolares foi revista e retomada para discussão por Castro Frade e Falcão (2007) e Falcão (2008).

O ponto crucial, ressaltado pelos trabalhos do grupo de psicólogos da Educação Matemática de Recife durante a década de oitenta do século passado, e que tem interesse para a presente discussão, diz respeito a uma expectativa que está na base dos projetos pedagógicos contemporâneos, tanto em termos de organização programática de conteúdos como em termos de avaliação: a expectativa segundo a qual tudo o que se aprende na escola, além de inserir o aprendiz no mundo formal dos conhecimentos, socialmente valorados e organizados, instrumentalizará este aprendiz para a vida extra-escolar, fornecendo-lhe ferramentas para seu bom funcionamento sócio-cultural mais amplo. Em poucas palavras, a expectativa segundo a qual a escola não é um mundo autocentrado e voltado para si mesmo, mas prepara e instrumentaliza “para a vida”. Nesse sentido, um exemplo recente, e dramaticamente bem-sucedido desse papel da escola, foi dado em 26 de dezembro de 2004, quando um tsunami¹ varreu as costas de vários países asiáticos; nesta ocasião, uma garotinha britânica de onze anos, Tilly Smith, ao ver o recuo do mar que precede a onda gigante, na praia tailandesa de Khao Lak, lembrou lição escolar recente na qual a sua professora havia discorrido sobre tsunamis, mencionando que o recuo do mar era prenúncio da onda gigante. A menina, numa iniciativa que com certeza encheu de orgulho sua professora, advertiu a família e várias pessoas ao redor acerca do que estava por acontecer e, com isso, salvou da morte não só sua família, mas quase cem pessoas, tendo sido por isso apelidada à época, pela imprensa internacional, de “o Anjo da Praia” (cf. O Verbo, 2005). Ora, nem sempre, infelizmente, esse bem sucedido trânsito entre a escola e o mundo extra-escolar se verifica, notadamente nos domínios da Educação Matemática. A transposição de habilidades e competências (termos que serão retomados mais adiante) da escola, para outros contextos sócio-culturais, tem-se mostrado bastante problemática, conforme evidenciam dados de avaliações institucionais: um estudo realizado pelo Sistema Nacional de Avaliação da Educação Básica (SAEB, 2001), mostrou que dois terços dos estudantes brasileiros concluem o ensino médio com ‘nível crítico’ de raciocínio matemático. Ou seja, a maioria dos jovens que chega ao mercado de trabalho não tem condições de resolver cálculos e equações básicas (apesar de que, de alguma forma não-reconhecida escolarmente, “sobrevivem” às exigências computacionais do mundo extra-escolar, notadamente quando se trata de lidar com dinheiro). Os dados de desempenho dos estudantes brasileiros ficam ainda mais dramáticos quando contextualizados internacionalmente: no ano de 2000, o Programa Internacional de Avaliação de Alunos (PISA, na sigla em inglês) mediu o desempenho de crianças de quarenta e um países diferentes: o teste mostrava quais delas estavam absorvendo e aplicando, de maneira mais adequada, os conteúdos de Matemática e de Ciências - o Brasil ficou em penúltimo lugar. Em 2007, novos resultados: num total de cinqüenta e sete países, o Brasil ficou em 53º lugar na avaliação relativa à Matemática (PISA, 2008).

Os pontos discutidos acima remetem a uma questão controversa, que tem ocupado uma larga comunidade pluridisciplinar: a avaliação de desempenho escolar. A Psicologia tem feito contribuições importantes, através de sub-domínios como a Psicometria e a Psicologia Cognitiva (Primi et al., 2001). Em termos de Psicologia Escolar e Psicopedagogia, as contribuições de Phillippe Perrenoud (PERRENOUD, 2004; 1999) tiveram especial impacto em termos das idéias que embasam os principais instrumentos de avaliação brasileiros, como o SAEB (Sistema de Avaliação do Ensino Básico), ENEM (Exame Nacional do Ensino Médio), ENCCEJA (Exame Nacional para Certificação de Competências para Jovens e Adultos), Prova Brasil e Provinha Brasil (INEP, 2008). Buscaremos aqui contribuir, brevemente, para esse debate, tentando manter como foco de análise as avaliações de desempenho escolar em Matemática, a partir da ótica da Psicologia.

2 Pressupostos da Psicologia da inteligência e da Psicometria para o processo de avaliação de competências cognitivas

Em termos gerais, a avaliação busca ter acesso a amostras de desempenho, por meio das quais, como em qualquer procedimento baseado em amostragem, se possam estabelecer generalizações acerca de desempenho que vão além da amostra utilizada. Tal amostra de desempenho é acessada através de determinado instrumento de avaliação construído para este fim. A figura 1, a seguir, ilustra esquematicamente o que consideramos serem as quatro etapas cruciais a considerar no planejamento e execução de determinado procedimento de avaliação de desempenho escolar. Cada uma das etapas referenciadas acima abarca um rol considerável de pressupostos teóricos acerca de aprendizagem, desenvolvimento, organização do domínio de conteúdo (em nosso caso, Matemática) e operacionalização metodológica na construção, aplicação e interpretação do instrumento. Comentamos, a seguir, cada uma dessas quatro etapas, de forma a fornecer subsídios acerca da importância e complexidade de cada uma delas:

- Etapa 1: circunscrição de determinada competência (ou rol de competências) a avaliar: trata-se aqui de estabelecer o que se quer, efetivamente, avaliar, partindo-se do pressuposto de que avaliações são necessariamente focais, mesmo que esse foco varie, desde itens programáticos de determinado nível de ensino (como a prova de unidade proposta por determinado professor de Matemática) até a avaliação de todo um ciclo de ensino, como por exemplo, uma avaliação de todo o ciclo de ensino fundamental. Seja como for, cabe aqui uma primeira e crucial decisão, a ser tomada tendo-se em mente elementos de uma dupla natureza: a) Quais conteúdos matemáticos se espera (sócio-institucionalmente) que devam ter sido ensinados, o que vai forçar o propositor da avaliação a levar e conta aspectos de transposição didática (CHEVALLARD, 1985; PERRENOUD, 1998; ARSAC et al., 1994), ou seja, que pontos do arcabouço de conhecimentos da Matemática enquanto saber de referência, uma vez transpostos de seu contexto de formulação para o contexto de ensino, deveriam ter sido ensinados e portanto deverão ser avaliados? b) Trata-se, aqui, de injunções pragmáticas, da ordem do realismo circunstancial do dia-a-dia do professor e da escola: quais os conteúdos matemáticos que se pôde ensinar, e portanto que pontos a avaliação poderá verificar? Enfim, nessa primeira etapa da avaliação são tomadas decisões de recorte do domínio de conhecimentos matemáticos a serem circunscritos como foco. Nesse sentido, poderíamos denominar essa etapa, para efeito de síntese, de etapa do conteúdo matemático.

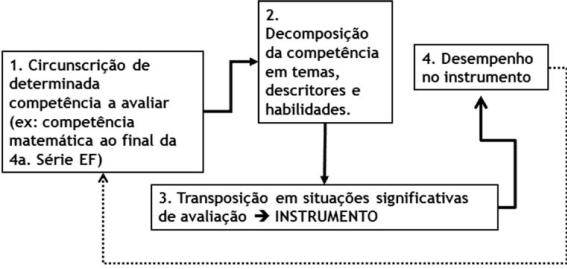
Figura 1:
Fluxo básico de trabalho na preparação e aplicação de instrumento de avaliação de desempenho escolar

- Etapa 2: decomposição da competência em temas, descritores e habilidades: o domínio de determinados conteúdos matemáticos se traduz, para efeito de avaliação, em competências cognitivas. Conforme aludido acima, este é um construto teórico controvertido e bastante discutido em vários domínios da Psicologia; neste debate, Perrenoud representa um marco de contribuição importante, com a proposta do conceito de competência e dos conceitos associados de habilidades (PERRENOUD, 1997; 1999). Para este autor, as competências, em seu sentido mais amplo, referem-se a amplas capacidades cognitivo-instrumentais, passíveis de utilização transdisciplinar em várias áreas específicas de conteúdo. Assim, a pesquisa em Psicologia da inteligência (notadamente aquela de orientação psicométrica) forneceu à Psicopedagogia a idéia da circunscrição de um número restrito de competências gerais, articulado com um outro conjunto mais extenso de habilidades ou competências específicas.

Em livro recente acerca da competência geral do professor do ensino fundamental, por exemplo, Perrenoud propõe organizar tal competência global em dez competências gerais ² e quarenta e quatro competências específicas (PERRENOUD, 2004). Ora, essa perspectiva teórica tem todo um embasamento de pesquisa no domínio da Psicologia da inteligência, e merece um breve comentário.

P. W. Schelini, pesquisadora brasileira, com interesse na modelização psicométrica da inteligência humana, faz expressiva retrospectiva histórica em relação aos modelos que têm sido propostos para esse construto desde a década de quarenta do século passado (SCHELINI, 2006). Segundo esta autora, remonta a C. Spearmann a proposição pioneira de um modelo dicotômico ou bi-fatorial de inteligência, que propunha uma inteligência geral (evidenciada por um fator descritivo de maior poder de resumo da variância de respostas, e por isso denominado de fator G), e fatores específicos mais focais, denominados de fatores S). P. W. Schelini observa que “[...] o fator de inteligência geral, subjacente a todas as atividades intelectuais, representaria uma espécie de energia, com base neurológica, capaz de ativar a capacidade de realização de trabalhos intelectuais”, enquanto que “[...] os fatores específicos seriam relativos a uma tarefa específica, representando particularidades de cada instrumento” (SCHELINI, 2006, p. 323). A idéia do fator G, ainda segundo Schelini (2006, p. 323-324), encontrou resistência representada, especialmente, por Louis Thurstone, para quem não haveria indícios suficientes na formulação de Spearmann para sustentar a idéia de um único fator que embasasse toda a grande pluralidade de tipos de desempenho intelectual. Thurstone, após analisar fatorialmente itens de testagem de inteligência na década de trinta do século passado, propôs a existência de pequeno número de fatores independentes, referentes a nove “capacidades mentais primárias”, excluindo desse modelo um fator geral de inteligência.

O terceiro momento desse processo histórico foi representado por um esforço de conciliação de uma perspectiva fundada na ênfase em um fator geral e outra perspectiva com ênfase em fatores específicos de inteligência. Este terceiro momento conduziu a uma formulação teórica que nos interessa de perto, aqui, tendo em vista seu impacto atual sobre os modelos brasileiros de avaliação de desempenho escolar (PRIMI et al., 2001; PRIMI, 2003) trata-se da proposição, inicialmente formulada por Raymond Cattell, de um modelo de inteligência abarcando agora doisfatores gerais de inteligência: uma “inteligência fluida” (fluid intelligence, Gf), e uma inteligência cristalizada (crystallized intelligence, Gc).

R. Primi e colaboradores resumem com bastante clareza as características centrais de cada uma dessas duas modalidades de inteligência geral (PRIMI et al., 2001, p. 157) a inteligência cristalizada priorizaria o conhecimento acumulado pelo indivíduo e culturalmente transmitido, principalmente via escolarização, conhecimento esse que, geralmente, seria mobilizado para a resolução de problemas semelhantes aos que se aprendeu no passado; a inteligência fluida priorizaria o raciocínio, a capacidade de processamento cognitivo, isto é, a capacidade geral de processar informações (por exemplo, relacionar idéias complexas, formar conceitos abstratos, derivar implicações lógicas a partir de regras gerais), quando se resolvem problemas relativamente novos, para os quais existem poucos conhecimentos previamente memorizados e disponíveis. Esse modelo teórico, de dois fatores gerais com as características acima mencionadas, está na base da proposição de distinção entre competências (associáveis a formas de inteligência fluída, por seu caráter mais amplo e mais independente de conteúdos informacionais propriamente ditos) e habilidades, relacionadas a caminhos de operacionalização específicos, em contextos específicos.

A consideração da competência cognitiva global humana, em termos de competências e habilidades, encontra alento renovado na evolução, em Psicometria, do modelo Gf-Gc de Cattel, posteriormente validado por John Horn, (SCHELINI, 2006, p. 324) para a Teoria dos Três Estratos, de John Carroll. Este autor procedeu à reanálise estatística (notadamente análise multidimensional hierárquica) de 460 conjuntos de dados anteriormente coletados (SCHELINI, 2006, p. 325), propondo um modelo para o funcionamento cognitivo humano em três camadas hierarquicamente organizadas, conforme esquematizado pelas Figuras 2 e 3 abaixo:

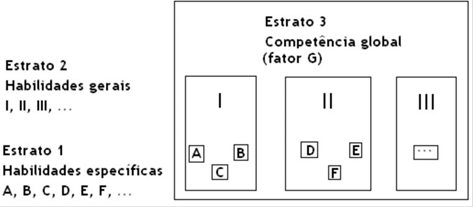
Figura 2:
Esquema ilustrativo da proposta hierárquico inclusiva da Teoria dos Três Estratos para o funcionamento cognitivo humano

O esquema proposto na Figura 2 acima se desdobra na representação proposta pelo quadro a seguir, com maior nível de detalhamento. Ao olhar para o resumo da Teoria dos Três Estratos, proposto pelo Quadro 1, cabe um comentário da ordem da Psicologia da Educação Matemática, a partir destas contribuições da pesquisa psicométrica de modelos da inteligência humana: podemos verificar que o “raciocínio quantitativo”, aspecto crucial para a atividade matemática (e portanto, supõe-se, para a avaliação de desempenho em Matemática), acha-se inserido no domínio da “inteligência fluida”. Ora, tal detalhe tem conseqüências inegáveis em termos de montagem de instrumentos de avaliação: se se considera que a inteligência fluida faz parte daqueles aspectos do funcionamento cognitivo, menos conectados a informações e conteúdos, e mais ligados a operações mentais abstratas, então o aspecto crucial do desempenho em Matemática seria da ordem do raciocínio abstrato, e não do conhecimento conteudístico-informacional-procedural. Convém, a esse respeito, assinalar, desde logo, que esta não é uma questão resolvida ou esgotada em Psicologia da inteligência, pois a vertente mais recente em termos de modelização psicométrica da inteligência propõe, com o chamado modelo de integração CHC (Cattel-Horn-Carrol) (SCHELINI, 2006, p. 326; PRIMI, 2003, p. 68-69; IAP, 2008), que o que poderíamos aqui chamar amplamente de “competência matemática” teria componentes no âmbito da inteligência fluida (o chamado “Raciocínio quantitativo – RQ”,), mas abarcaria um outro fator geral complexo, o “Conhecimento quantitativo – Gq”, no âmbito do qual deveriam ser considerados, de forma distinta, o “Conhecimento matemático – KM” e o “Desempenho em matemática – A3” (conforme Quadro 2 abaixo):

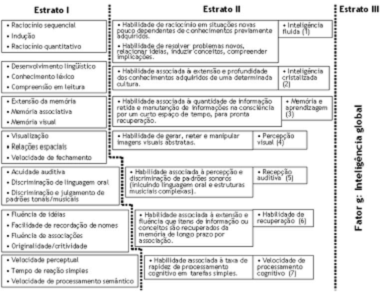
Quadro 1
Esquema desdobrado da proposta hierárquico-inclusiva da Teoria dos Três Estratos para o funcionamento cognitivo humano
Fonte: Elaborado a partir do esquema proposto por Primi et al. (2001, p. 154) e Schelini (2006, Anexo B, p. 331).

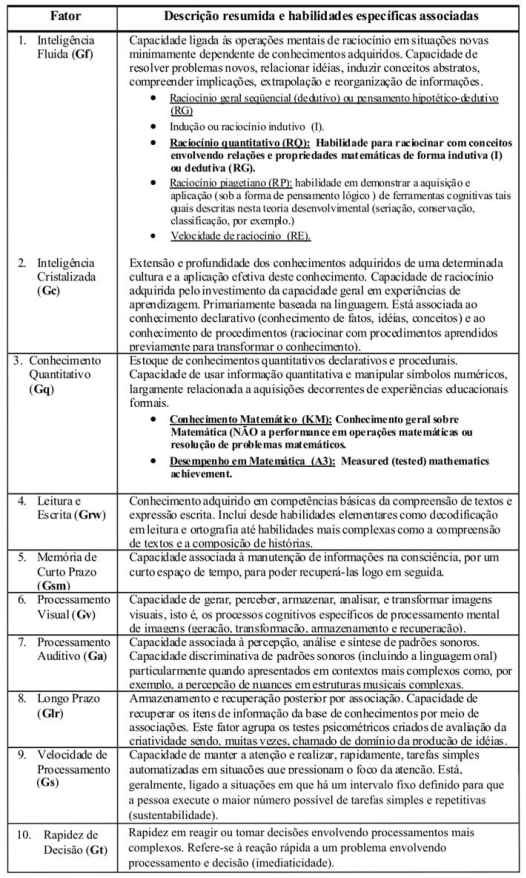
Quadro 2
Definição resumida dos dez fatores amplos da teoria CHC
Fonte: Modificado a partir de Primi, 2003, com informações suplementares oriundas de CHC Project, 2008, tradução nossa; destaques em negrito acrescentados.

Os propositores do modelo CHC, considerados por especialistas como o “estado da arte”, em termos de modelos psicométricos de organização e funcionamento da inteligência humana (PRIMI, 2003), chamam a atenção para o fato de que os estudos de análise fatorial dos itens de teste tratados evidenciaram que o “Raciocínio quantitativo – RQ” estaria separado do “Conhecimento quantitativo – Gq”. RQ faria parte da inteligência fluida, caracterizando-se pela capacidade de raciocinar, indutiva ou dedutivamente, no âmbito da resolução de problemas matemáticos. Gq, por sua vez, parece uma especialização da inteligência cristalizada (Gc), focalizada no âmbito dos dados conteudísticos da Matemática; nesse sentido, Gq abarcaria o conhecimento matemático (KM), ou seja, o conjunto de conceitos e procedimentos acumulados pelo indivíduo, habilidade que por sua vez se demarcaria do “Desempenho em Matemática – A3”, representado pela performance do indivíduo em testes de desempenho em Matemática.

Esse último dado merece especial atenção de nossa parte, educadores matemáticos e psicólogos da Educação Matemática: os dados de desempenho em instrumentos de avaliação analisados pelos propositores do modelo CHC têm sua própria autonomia, não se correlacionando com “raciocínio quantitativo” (RQ) ou “Conhecimento matemático” (KM) a ponto de se mesclar com tais competências; em outras palavras, sair-se bem em avaliações com instrumentos em Matemática seria uma competência cultural específica, aprendida na escola (no mais das vezes de forma implícita ou metacognitiva), o que, inclusive, remete às reflexões de Lave e Wenger acerca da inserção do aluno numa “comunidade de praticantes de Matemática” como aspecto crucial para o bom desempenho escolar em matemática (LAVE; WENGER, 1991), bem como às contribuições de G. Brousseau em termos da noção de “contrato didático” (BROUSSEAU, 1998).

Em resumo, se de fato o modelo teórico CHC tiver a robustez e validade defendida por seus propositores, a competência global em Matemática abarcará: a) Aspectos de raciocínio relacionados à inteligência fluida, ou seja, a capacidade de raciocínio abstrato indutivo e dedutivo; b) aspectos próximos da inteligência cristalizada, representados pelo acervo de conhecimentos matemáticos (Gq), conhecimentos esses divididos em dados conceituais (como o próprio conceito de número), procedurais-declarativos (como os algoritmos) e meramente informacionais (como o conhecimento lingüístico dos rótulos dos números), e ainda c) o conhecimento acerca dos próprios instrumentos de avaliação em Matemática (A3) (como por exemplo “problemas que falam da soma e da diferença das idades de pai e filho se resolvem com um sistema de equações, com simplificação por adição”, ou ainda: “problemas que falam em ‘ganhar’ são problemas que se resolvem com um conta de somar”, ou ainda “numa avaliação é importante trabalhar rápido”). Em última análise, para ser “bom” em Matemática seria preciso dispor de raciocínio lógico-operatório abstrato (do tipo explorado nas tarefas piagetianas e em itens de testes psicométricos como o Raven), dispor de conhecimentos matemáticos e dispor de conhecimentos acerca dos instrumentos de avaliação (este último dado, como todos sabem, é amplamente conhecido pelos chamados “professores de cursinho” e “professores de concurso”, que explicitam para seus alunos informações acerca do perfil de construção/expectativas/tipos de pergunta dos instrumentos de avaliação a que seus alunos submeter-se-ão).

Em relação às propostas do modelo CHC e suas conseqüências para a reflexão acerca da competência matemática global (e sua avaliação), resumidas e discutidas acima, caberia, a esta altura, a seguinte questão: se é verdade, como propõe este modelo, que “[...] o conhecimento quantitativo – Gq representa o acervo individual acumulado de conhecimento matemático, e não a capacidade de raciocinar com/a partir deste conhecimento”³, qual instância do funcionamento cognitivo seria responsável justamente por essa importante operação de natureza metacognitiva que seria a sinergia de raciocínio lógico voltado para conteúdos matemáticos conhecidos no âmbito de um procedimento cultural específico, com regras próprias (o teste ou contexto de avaliação)? A resposta que vem da comunidade de pesquisa de inspiração teórica enraizada na inteligência artificial propõe a idéia de “gestores metacognitivos de alto nível”, como é o caso das formulações clássicas de R. J. Sternberg, para quem a tarefa cognitiva de resolução de problemas comportaria cinco componentes ou etapas seqüenciais de tratamento: codificação, inferência, mapeamento, aplicação, resposta e justificativa (STERNBERG, 1977). As três primeiras etapas (codificação, inferência, mapeamento), dentre as cinco listadas acima, seriam de especial importância para o desencadeamento do processo integrado de resolução de problemas. Os propositores do modelo CHC, por outro lado, confrontados a questões de gestão metacognitiva como a que formulei acima, tendem a recorrer, mais uma vez, à explicação fundada em um “fator G”, agora contudo, de natureza bastante mais complexa do que nas suas primeiras formulações (tratar-se-ia agora de um fator responsável por competência integrativa, gestão metacognitiva das demais competências). R. Primi chama a atenção para o fato de que, atualmente, nenhuma das baterias psicométricas disponíveis contemplaria a detecção de um tal fator G, pois o que antes era assimilado ao fator G (raciocínio formal-abstrato pouco vinculado à linguagem, aprendizagens, contextos culturais) seria agora assimilado à idéia de inteligência fluida, um dos dez fatores componentes do modelo CHC (PRIMI, 2003).

De fato, parece-nos que a consideração monológica do indivíduo, enquanto tal para a modelização do funcionamento cognitivo, leva a um impasse teórico, quando confrontado a facetas do funcionamento mental como consciência e metacognição. Mas há outros problemas a considerar: a proposição de conceitos como “conhecimento declarativo” (Quadro 2) parece reduzir tais conceitos a seu aspecto taxonômico mais simples, distante da complexidade dos conceitos em contextos como o matemático. Nossa perspectiva teórica acerca dos conceitos (e muito especialmente acerca dos conceitos matemáticos) propõe que conceitos não são entidades autônomas e circunscritas em si mesmas, mas modelos mentais articulados em campos conceituais. Esclarecemos, desde já, que a acepção teórica de “campos conceituais” aqui proposta é aquela formulada por Gérard Vergnaud, no contexto de sua teoria dos campos conceituais (VERGNAUD, 1990). Segundo tal proposta, ilustrada pela Figura 3, abaixo, um determinado conceito A (1) não pode ser concebido a não ser em relação com outros conceitos (2), no âmbito de um campo conceitual; tal campo conceitual poderá sofrer recortes para ensino e avaliação (3) e, no caso específico do ensino, poderá, igualmente, ser seqüencializado em termos de um ordenamento temporal de conteúdos (4).

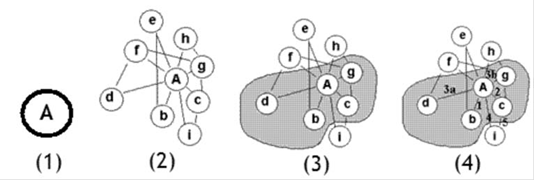
Figura 3:
Ilustração da idéia teórica de campos conceituais e seu interesse para o ensino e para a avaliação
Fonte: VERGNAUD, 1990; 1997; FALCÃO, 2003, p. 39.

No domínio da avaliação, os conceitos que compõem determinado domínio de competência matemática são freqüentemente denominados temas (INEP, 2008). Tais temas, em articulação, compõem então um campo conceitual, conforme ilustrado pela Figura 4 abaixo:

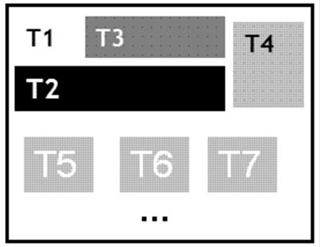
Figura 4:
Ilustração de campo de temas representativo de determinada competência matemática

Se pensarmos novamente aqui, à guisa de exemplo, em competência algébrica, poderemos listar os seguintes temas (conceitos) constituintes desse campo conceitual: incógnita, variável, equivalência algébrica, equação algébrica, raiz de equação. Para efeito de ensino ou avaliação, pode-se construir um campo conceitual representativo da competência que se deseja ensinar/avaliar com maior ou menor extensão, conforme ilustrado pela Figura 2, item (3) acima. Uma vez estabelecido o campo de temas (ou campo conceitual) para determinada competência matemática, o passo seguinte diz respeito à escolha de descritores, conforme ilustrado na Figura 5, a seguir. Tendo sempre como exemplo de referência a competência algébrica e seus temas componentes, poder-se-ia tentar estabelecer, para cada um desses temas, determinados descritores que permitissem a operacionalização de exemplos de ensino e de itens de avaliação. Descritores são, portanto, atividades (tarefas, questões, problemas) que têm vinculação demonstrável com cada tema constituinte de um campo de temas. Tal vinculação resulta de esforço de reflexão epistemológica, acerca do campo conceitual em jogo, de forma que cada descritor tenha efetivamente vínculo com aspectos cruciais do campo de temas. Nesse sentido, um descritor representa uma “sonda” considerada eficaz para prospecção avaliativa de determinados temas, os quais, por sua vez, devem (ou deveriam) traduzir determinadas competências e habilidades. Cada descritor busca portanto “[...] uma associação entre conteúdos curriculares e operações mentais desenvolvidas pelos alunos que traduzem certas competências e habilidades”, prestando-se portanto para a construção de itens de testes de avaliação (INEP, 2008).

Aqui, mais uma vez, o domínio do conteúdo matemático por parte do professor-avaliador é crucial, pois a escolha adequada de descritores para temas guarda relação com a competência deste professor no sentido de: a) ter clareza epistemológica acerca de determinado conteúdo temático da Matemática (por exemplo, variável algébrica), e b) ter clareza acerca de que situação-problema pode representar, adequadamente, os principais aspectos envolvidos nesse tema. Na ilustração a seguir (Figura 5), se pensarmos que T3 representa o tema variável algébrica, os descritores d3a e d3b associados a T3 poderiam ser tarefas de completação de tabelas (d3a) (ilustrado pela Figura 6) e de construção de gráficos cartesianos a partir de dados tabulados (d3b) (ilustrado pela Figura 7).

- Etapas 3 e 4: proposição de instrumento de avaliação e desempenho no instrumento: conforme proposto na Figura 1, as etapas seguintes, na presente discussão, dizem respeito à proposição de instrumento completo de avaliação, a partir da proposição de uma série de itens conectáveis a descritores de competências e habilidades matemáticas. Conforme discutido em seções anteriores do presente artigo, a proposição de um instrumento de avaliação comporta pressupostos importantes, acerca do domínio de conhecimento focalizado, bem como das operações cognitivas necessárias ao acesso funcional a tal domínio (operações descritas em termos de competências e habilidades). Um terceiro aspecto a considerar, e que não será aqui tratado, posto estar fora do escopo estabelecido para este artigo, diz respeito a um conjunto de requisitos técnicos para a elaboração de um instrumento de avaliação de competências cognitivas, ou seja, aspectos referentes à sua validade (KANE, 2001). Estes três aspectos considerados, espera-se que o desempenho no teste seja indicativo das competências e habilidades focalizadas pelos descritores e itens de avaliação propostos.

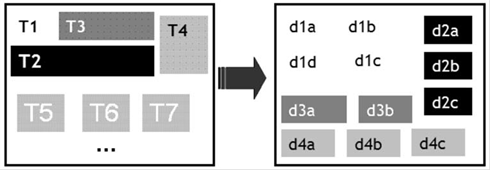
Figura 5:
Ilustração de campo de temas representativo de determinada competência matemática associado a conjunto de descritores para cada tema

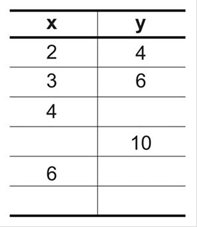
Figura 6:
Exemplo de item de instrumento de avaliação conectado a um dos descritores do tema matemático variável algébrica (d3a): Questão a ser proposta: tendo em vista a regra inerente à relação de cada valor de x com o respectivo valor em y preencher as células em branco

Tais considerações encerram aspectos referentes à interlocução da avaliação com a Psicologia da Inteligência e Psicometria, passando-se, na seção seguinte, a considerações adicionais de ordem teórica, especificamente oriundos da Psicologia da Educação Matemática, com desdobramentos para a avaliação.

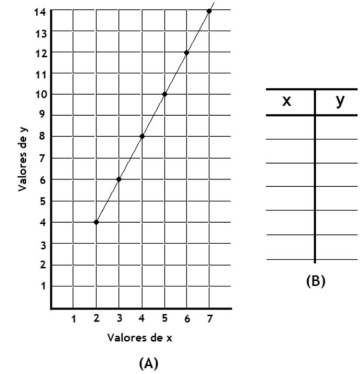
Figura 7:
Exemplo de item de avaliação conectado a um dos descritores do tema matemático “variável algébrica” (d3b): Questão a ser proposta: tendo em vista a regra inerente à relação de cada valor de x com o respectivo valor em y, representada pela reta traçada no plano cartesiano por par de valores de x e y (A), preencher as células em branco da tabela (B)

3 Pressupostos teóricos da Psicologia da Educação Matemática para o processo de avaliação de competências cognitivas

Nesta parte final das presentes considerações, pretendemos oferecer contribuições oriundas de nossa própria reflexão no âmbito da Psicologia da Educação Matemática, retomando pontos que nos parecem especialmente importantes (FALCÃO, 2003; 2007; 2008; FALCÃO et al., 2007; FRADE, FALCÃO, 2008) para esta reflexão, cujo ponto de foco é a avaliação de competências em Matemática. Para efeito de organização de idéias, esta seção será dividida em sub-tópicos, que deverão recobrir, nesta ordem, aspectos relacionados à perspectiva teórico-epistemológica da própria abordagem psicológica das competências cognitivas, abrangência e complexidade da atividade matemática, concluindo-se com uma tentativa de explicitar, resumidamente, qual seria o perfil do “aluno-padrão de Matemática”, ou seja, quais os requisitos considerados desejáveis para se considerar que um aluno atingiu todos os objetivos cruciais de capacitação e desempenho em Educação Matemática.

3.1 Aspectos teórico-epistemológicos cruciais para a abordagem psicológica das competências cognitivas humanas

Nosso pressuposto fundador, premissa básica de todas as reflexões que virão em seguida, estabelece que o conhecimento é produto da ação sobre o mundo, com sua recíproca: a verificação pelo sujeito dos resultados desta ação. Se por um lado é verdade que a “voz” (no sentido bakhtiniano do termo) de Piaget ressoa claramente aqui (PIAGET, 1973; 1990), é preciso que se diga, desde já, que outras heranças serão igualmente incorporadas.

Várias abordagens em Psicologia fazem seu foco sobre o indivíduo, seja em termos de seu aparato neurofisiológico, seja em termos de seu acervo de comportamentos observáveis, seja em termos de suas instâncias de funcionamento intrapsíquico; outras abordagens têm o cuidado de estabelecer a interação do indivíduo com entes do mundo que o cerca, sejam esses entes objetos do mundo físico ou mesmo outros indivíduos. Todas estas perspectivas referidas aqui têm como ponto em comum, do ponto de vista teórico-epistemológico, a proposição de uma abordagem monológica do indivíduo humano (isso é válido mesmo para muitos daqueles que apresentam em seu discurso a palavra-chave “interação”, conforme será discutido em seguida). É considerada monológica a abordagem psicológica que se atém e se satisfaz com a observação do indivíduo para a construção de conhecimento psicológico, e mesmo no caso em que observa grupos de indivíduos, estabelecem delimitações claras entre tais indivíduos, de forma que o grupo observado resulta da conjunção de indivíduos isolados, que se comunicam, trocam informações, agem e reagem mas não se co-constituem (MARKOVÀ, 2006). Falar, alternativamente, numa perspectiva dialógica para a abordagem das competências cognitivas humanas significa propor uma interdependência entre o conhecimento compartilhável individual e social, e entre estabilidade e mudança, entendendo-se a dialogicidade como “[...] a capacidade da mente humana de conceber, criar e comunicar realidades sociais em termos de outro indivíduo” (FALCÃO, 2008, p. 119). Nesse sentido, uma teoria psicológica do conhecimento humano deve captar processos de co-construção de aspectos sócio-culturais e individuais. Para Ragnar Rommetveit, tal esforço se justifica na medida em que se considera que o conhecimento não pode ser circunscrito aos limites da pele, da caixa craniana ou mesmo da mente de determinado indivíduo, pois tal conhecimento deve ser visto como socialmente distribuído, o que é particularmente verificável, por exemplo, em processos psicológicos como a memória, o raciocínio, a resolução de problemas (ROMMETVEIT, 2003).

A conseqüência direta da perspectiva acima é que não se pode separar a análise da aprendizagem e do desenvolvimento cognitivo da análise da experiência cultural do sujeito, na qual se incluem as experiências escolares e extra-escolares. As relações humanas, diferentemente das relações entre animais não-humanos, não podem se resumir a um par de sujeitos (um que age, outro que reage), mas envolvem necessariamente três pólos, quais sejam um signo, um objeto a que este signo se refere e um intérpretedeste signo (FALCÃO, 2008). Em outras palavras, o processo de interação entre um indivíduo e outro (que está por exemplo na base dos processos de ensino e aprendizagem), ou entre um indivíduo e um objeto, não pode ser concebido como um processo de contato direto como o de “ação-reação” acima aludido: tal interação é, necessariamente, mediada por uma atividade de construção de significado, de natureza e origem sócio-histórico-cultural. Nesse sentido, toda e qualquer atividade humana seria, necessariamente, mediada, pois os objetos destas atividades jamais seriam determinados por suas relações “diretas” com os “organismos” (indivíduos envolvidos), mas por suas relações mediadas por contextos, expectativas, histórias pessoais, enfim, por toda uma gama de possibilidades de funcionamento cognitivo decorrentes da função semiótica da linguagem (LEONTIEV, 1977, p. 66-67).

3.2 Abrangência e complexidade da atividade matemática

Uma vez caracterizada como atividade humana mediada, portanto enraizada em contexto sócio-histórico-cultural de situações e artefatos de mediação (amplificadores culturais (BRUNER, 1997) ou “próteses culturais” (HAZIN, 2006)), cabe agora refletir acerca da pluralidade de contextos em que se exerce tal atividade. Pelos menos três contextos de atividade são distinguíveis para o exercício de atividade matemática: em primeiro lugar, os já referidos contextos escolar e extra-escolar, cujas diferenças e complementaridades têm sido descritas e exploradas desde o início do século passado (PIAGET, 1974).

Cada um desses contextos tem suas especificidades, as quais influem, intensamente, nos caminhos de emergência (e portanto de avaliação) da atividade matemática. O contexto escolar é regido pelos já referidos contratos didáticos (fundados, por sua vez, em sistema de crenças e premissas explícitas e implícitas), em função dos quais determinados obstáculos didáticos (BACHELARD, 1996) importantes poderão ser construídos: assim, a excessiva ênfase em atividades aritméticas, no início do ensino fundamental, pode se constituir na responsável por obstáculo importante à introdução ao pensamento algébrico (FALCÃO, 1996; 1997).

Em contexto extra-escolar, por outro lado, operações matemáticas pouco exploradas, escolarmente, ganham grande relevo, como é o caso da estimativa, do cálculo mental, do uso preferencial de ordens de grandeza a números exatos (aproximações) no pensamento quantitativo.

Há, ainda, um terceiro contexto, ao lado dos dois acima referidos, que merece menção: trata-se do contexto formal, ou contexto de produção do saber, denominado pela tradição francófona de contexto do “saber-sábio” (“savoir-savant”) (CHEVALLARD, 1985). Este é o contexto acadêmico onde militam os matemáticos-cientistas, aqueles encarregados não somente do uso, mas sobretudo, da produção e da meta-reflexão sobre a Matemática, aqui considerada como domínio formal e socialmente regulado de saber. Tal contexto tem, igualmente, suas regras e características próprias, como bem assinalado por estudos sociológicos voltados para “a vida dos laboratórios acadêmicos” (LATOUR, 2000), assim como, atribuições específicas, como a já referida tarefa de transposição didática. Nesse contexto, se consideramos, como G. Brousseau, que a atividade Matemática comporta três tipos distinguíveis de situações de ação, o contexto da matemática formal se voltará, com especial ênfase, para as situações de validação (fornecimento de provas da veracidade de um enunciado, via demonstração matemática, de forma a conseguir a adesão social-acadêmica) (BROUSSEAU, 1998). O contexto extra-escolar se caracterizará, fortemente, por situações de ação, voltadas para a instrumentalização da Matemática em contextos de funcionamento sócio-cultural específico (comércio, por exemplo), cabendo à escola a ênfase sobre situações de formulação, voltadas para o desenvolvimento de regras lexicais, taxonômico-conceituais e “gramaticais” de formulação matemática.

3.3 Perfil do “aluno-padrão de Matemática”

A massa crítica que acumulamos até aqui nos permite tentar formular qual seria o “aluno padrão” ou ideal em Matemática, aquele que gostaríamos de produzir em nosso sistema de ensino, e que, portanto, guiaria, em mais alto nível, a montagem de nossos instrumentos de avaliação. Aliás, todo e qualquer instrumento de avaliação possui, implícito ou explícito, um tal perfil de desejabilidade; no Brasil, por exemplo, os Parâmetros Curriculares Nacionais (PCN, MEC, 1997) trazem subsídios fartos acerca das expectativas vigentes em termos de objetivos a atingir. Tendo em vista os pontos discutidos aqui, o perfil ideal de aluno de Matemática abarcaria os seguintes aspectos:

• capacidade de transitar, matematicamente, entre a escola e o mundo exterior à escola nos dois sentidos, o que implica a habilidade de aplicar ferramentas matemáticas em situações do cotidiano, bem como, modelizar situações reais do cotidiano em linguagem matemática;

• na escola, capacidade de fazer a Matemática transitar por outras disciplinas;

• motivação e disponibilidade para enculturar-se, matematicamente, o que implica desenvolver familiaridade com regras de pensamento matemático, dispor de bons interlocutores-mediadores (professores, colegas, membros do grupo familiar), dispor de bons artefatos de mediação (amplificadores e/ou próteses culturais), dispor de acervo de conhecimentos matemáticos e de conhecimentos em relação às regras (explícitas e implícitas) da comunidade de praticantes da sala de aula de Matemática;

• motivação e disponibilidade para pensar metamatematicamente: desenvolver capacidade de estimativa em situações pertinentes da cultura, recorrendo a senso numérico e conhecimento factual; habilidade metacognitiva em saber avaliar o grau de dificuldade de um problema antes mesmo de iniciar a resolução do mesmo;

• desenvolvimento de crenças e representações, afetivamente positivas, acerca da Matemática e da classe de Matemática (incluindo o professor e a si próprio como participante dessa comunidade), bem como de motivações, atitudes e emoções, igualmente positivas em relação à Matemática.

Tais perfis, obviamente, remetem à desejabilidade, não à realidade. Têm, contudo, o interesse de explicitar aqueles pontos que são considerados indispensáveis como objetivos a atingir (e portanto avaliar) quando se trata de oferecimento do que se pode pensar de melhor em termos de Educação Matemática.

4 Considerações finais

Procuramos, no presente artigo, oferecer subsídios à discussão acerca da avaliação de competências cognitivas em Psicologia, buscando, para isso, sistematizar possíveis contribuições da Psicologia, notadamente da Psicologia da Inteligência, Psicometria e Psicologia da Educação Matemática. Conforme muitos de nós, pesquisadores em Educação Matemática, enunciamos, seguidamente, que o domínio da Educação Matemática se constitui, necessariamente, em espaço interdisciplinar de concatenação de esforços, e a Psicologia é um dos campos de saber que tem contribuições específicas a dar. Tais contribuições, conforme discutiu-se aqui, têm relação com a proposição de um modelo teórico geral para o funcionamento cognitivo humano (inteligência, memória, percepção, formação de conceitos e demais processos cognitivos), em articulação com aspectos referentes à própria organização da Matemática, enquanto domínio de saber sócio-historicamente organizado e, epistemologicamente, circunscrito. Nesse sentido, procuramos esclarecer que a avaliação de desempenho é tarefa complexa, pois implica o estabelecimento prévio do modelo de funcionamento cognitivo em Matemática, ou seja, o estabelecimento de vínculos entre dois modelos complexos: o indivíduo que pensa e resolve problemas e a Matemática (separáveis apenas em tese, pois, de fato, trata-se, como unidade de análise, do indivíduo em atividade matemática).

Os modelos recentes fornecidos pela Psicologia da Inteligência tiveram impacto decisivo na circunscrição de competências e habilidades gerais, nas quais se acharia incluída a competência em Matemática. Tais modelos têm, sem dúvida, trazido iluminações sólidas, levantado novas questões e possibilitado avanços no que diz respeito à avaliação de competências cognitivas humanas. Não obstante o estado de robustez empírica e adesão ao modelo CHC de inteligência (CHC PROJECT, 2008; PRIMI, 2003), procurou-se evidenciar que tal modelo está longe de ter fechado a agenda de pontos de questionamento, acerca do funcionamento da inteligência humana, seja em termos de sua estrutura teórica interna (LAKATOS, 1987), seja em termos das limitações epistemológicas da teoria de sujeito humano subjacente ao quase-paradigma⁴ CHC.

Os modelos atuais de avaliação escolar, em geral, e avaliação matemática em particular, repousam, necessariamente, sobre concepções acerca de um sujeito humano fazendo Matemática. O grau de sofisticação com que tais modelos serão usados dependerá, sempre, do nível de tomada de consciência desse fato, por parte dos usuários-avaliadores. A circunscrição prévia de competências e habilidades matemáticas, marco de referência (na contemporaneidade) para o estabelecimento de iniciativas de avaliação, representa esforço de tradução operacional (no sentido do estabelecimento explícito da seqüência hierárquica competência-habilidade-descritores-questões de avaliação) de uma série de crenças e pressupostos teóricos. No presente artigo, assumimos posição nesse debate e apresentamos proposta extremamente resumida, quase que meramente enunciativa, do nosso rol de pressupostos e crenças teóricas; eles representam um esforço honesto de toda uma comunidade de pesquisadores, e por isso têm valor, mas certamente não têm a pretensão de ter atingido a verdade ou clarividência definitiva nesse domínio. Verdade e clarividência, de resto, fora do horizonte de possibilidades do fazer científico (FALCÃO; HAZIN, 2007).

Referências

ABREU, G. M. O uso da matemática na agricultura: o caso dos produtores de cana-de-açúcar. Recife, 1988. Dissertação (mestrado) Psicologia Cognitiva, Universidade Federal de Pernambuco.

ACIOLY, N. M. La juste mesure: une étude des compétences mathématiques des travailleurs de la canne à sucre du nordeste du Brésil dans le domaine de la mesure. Paris, 1994. Tese (doutorado), Université de Paris-5.

ACIOLY, N. M. A Lógica Matemática no Jogo do Bicho: compreensão ou aplicação de regras? Recife, 1985. Dissertação (mestrado) Psicologia Cognitiva, Universidade Federal de Pernambuco.

ARSAC, G. et al. La Transposition didactique à l’épreuve. Grenoble: La Pensée Sauvage Éditions, 1994.

BACHELARD, G. A formação do espírito científico. Rio de Janeiro: Contraponto, 1986.

BROUSSEAU, G. Théorie des situations didactiques. Grenoble: La Pensée Sauvage, 1998.

BRUNER, J. Atos de significação. Porto Alegre: Artes Médicas, 1997.

CARRAHER, T. N.; CARRAHER, D. W.; SCHLIEMANN, A. D. Na vida dez, na escola zero. São Paulo: Cortez, 1988.

CHC PROJECT Cattell-Horn-Carroll (CHC) Definition Project. Disponível em: http://www.iapsych.com/chcdef.htm. Acesso em: jul. 2008.

CHEVALLARD, Y. La transposition didactique. Grenoble: La Pensée Sauvage, 1985.

FALCÃO, J. T. R. Os saberes oriundos da escola e aqueles oriundos da cultura extra-escolar: hierarquia ou complementaridade? Saber & Educar, Porto, n. 13, p. 109-123, 2008.

FALCÃO, J. T. R. Conceptualisation en acte, conceptualisation explicite: quels apports théoriques à offrir à la didactique des mathématiques et des sciences? In: NUMA-BOCAGE, L.; MERRI, M.; VANNIER, M. P. Activité humaine et conceptualisation: questions à Gérard Vergnaud. Toulouse (France), Presses Universitaires du Mirail, 2007.

FALCÃO, J. T. R. Psicologia da educação matemática: uma introdução. Belo Horizonte: Autêntica, 2003.

FALCÃO, J. T. R. Lenguaje algebraico: un enfoque psicológico. Uno – Revista de Didáctica de las Matemáticas (Barcelona – Espanha). v. 14, p. 25-38, 1997.

FALCÃO, J. T. R. Clinical analysis of difficulties in algebraic problem solving among Brazilian students: principal aspects and didactic issues. Proceedings of the XXth International Conference for the Psychology of Mathematics Education. v. 2, p. 257-264, 1996.

FALCÃO, J. T. R; HAZIN, I. Dez mitos acerca do ensino e da aprendizagem de matemática. Pesquisas e práticas em educação matemática. v. 1, n. 1, p.27-48, 2007.

FRADE, C. Castro, FALCÃO, J. T. da Rocha. Exploring connections between tacit knowing and situated learning perspectives in the context of mathematics education. In: Watson, A., Winbourne, P. (Orgs.). New directions for situated cognition in mathematics education. London: Springer, 2008.

HAZIN, I. A atividade matemática de crianças com epilepsia idiopática generalizada do tipo ausência: contribuições da neuropsicologia e da psicologia cognitiva. Recife, 2006. Tese (doutorado), Programa de Pós-Graduação em Psicologia Cognitiva – UFPE.

IAP CHC theory. Disponível em: http://www.iapsych.com/IAPWEB/CHCTheory.html. Acesso em: jul. 2008.

INEP Instrumentos de avaliação da educação básica. Disponível em: http://www.inep.gov.br/. Acesso em jul. 2008.

KANE, M. T. Current Concerns in Validity Theory. Journal of Educational Measurement, v. 38, n. 4, p. 319-342, 2001.

KUHN, T. S. A estrutura das revoluções científicas. São Paulo: Perspectiva, 1978.

LAKATOS, I. La metodologia de los programas de pesquisa. Madrid: Alianza, 1987.

LATOUR, B. Ciência em ação. São Paulo: UNESP, 2000.

LAVE, J.; WENGER, E. Situated learning: Legitimate peripheral participation. New York: Cambridge University Press, 1991.

LEONTIEV, A. O desenvolvimento do psiquismo. São Paulo: Moraes, 1977.

LIMA, N. Carvalho. Aritmética na feira: o saber popular e o saber da escola. Recife, 1986. Dissertação (mestrado) Psicologia Cognitiva, Universidade Federal de Pernambuco.

MARKOVÀ, I. Dialogicidade e representações sociais: as dinâmicas da mente. Petrópolis: Vozes, 2006.

MEC. Ministério da Educação e do Desporto – Brasil. Parâmetros Curriculares Nacionais – 1 ciclo do ensino fundamental – Matemática. Brasília, Secretaria de Ensino Fundamental, 1997.

O VERBO. Menina britânica é recebida como heroína um ano após tsunami. Disponível em: http://www.overbo.com.br/modules/news/article.php?storyid=446. Acesso em jul. 2008.

PERRENOUD, P. La transposition didactique à partir de pratiques: des savoirs aux competences. Revue des sciences de l’éducation, v. 24, n. 3, 1998, p. 487-514. Disponível em: http://id.erudit.org/iderudit/031969ar. Acesso em: jul. 2008.

PERRENOUD, P . Diez nuevas competencias para enseñar. Barcelona, Graó, 2004.

PERRENOUD, P. Construir competências é viras as costas aos saberes? Pátio.Revista pedagógica. Porto Alegre, n. 11, p. 15-19, nov. 1999.

PERRENOUD, P. Construir as competências desde a escola. Porto Alegre: Artes Médicas, 1997.

PIAGET, J. Biologia e conhecimento: ensaio sobre as relações entre as regulações orgânicas e os processos cognoscitivos. Petrópolis: Vozes, 1973.

PIAGET, J. Epistemologia genética. São Paulo: Martins Fontes, 1990.

PIAGET, J. Réussir et comprendre. Paris: Presses Universitaires de France, 1974.

PISA. Program for international student assessment. Disponível em: http://www.pisa.oecd.org/pages/0,2987,en_32252351_32235731_1_1_1_1_1,00.html. Acesso em: jul. 2008.

POLYA, G. How to solve it. Princeton: Princeton University Press, 1973.

PRIMI, R. Inteligência: Avanços nos modelos teóricos e nos instrumentos de medida. Avaliação Psicológica, v. 1, p. 67-77, 2003.

PRIMI, R. Inteligência fluida: definição fatorial, cognitiva e neuropsicológica. Paideia, v. 12, n. 23, p. 57-75, 2002.

PRIMI, R et al. Competências e Habilidades Cognitivas: diferentes definições dos mesmos construtos. Psicologia: Teoria e Pesquisa, v. 17, n. 2, p. 151-15, 2001.

ROMMETVEIT, R. On the role of “a psychology ofthe second person” in studies of meaning, language, and mind. Mind, culture and activit, v. 10, n. 3, p. 205-218, 2003.

SAEB. Relatório SAEB 2001 – Matemática. Disponível em: http://www.inep.gov.br/basica/saeb/saeb_01.htm. Acesso em: jul. 2008.

SCHELINI, P. W. Teoria das inteligências fluida e cristalizada: início e evolução. Estudos de Psicologia 2006, v. 11, n. 3, p. 323-332. Disponível em: http://www.scielo.br/pdf/epsic/v11n3/10.pdf. Acesso em: jul. 2008.

SCHLIEMANN, A. D. Mathematics among carpenters and apprentices. In: DAMEROW, P. et al. (Eds.). Mathematics for all, Paris: UNESCO, 1984, p. 92-95.

STARNEWS. O que são tsunamis? Disponível em: http://www.starnews2001.com.br/tsunami/tsunami.html. Acesso em: jul. 2008.

STERNBERG, R. J. A component process in analogical reasoning. Psychological Review, v. 84, n. 4, p. 353-378, 1977.

VERGNAUD, G. The nature of mathematical concepts. In: NUNES, T.; BRYANT, P. Learningand teaching mathematics: an international perspective. London, Psychology Press, 1997.

VERGNAUD, G. La théorie des champs conceptuels. Recherches en Didactique des Mathématiques. v. 10, n. 23, p. 133-170, 1990.

Notas

Notas de autor