Artigos Originais
As demandas matemáticas da indústria petrolífera do Norte Fluminense
Mathematical demands of oil industry in the northern region of Rio de Janeiro
As demandas matemáticas da indústria petrolífera do Norte Fluminense
Vértices (Campos dos Goitacazes), vol. 18, núm. 2, pp. 75-96, 2016
Instituto Federal de Educação, Ciência e Tecnologia Fluminense
Recepción: 28 Septiembre 2015
Aprobación: 02 Febrero 2016
Resumo: A região Norte Fluminense tem, na indústria petrolífera, um forte empregador de mão de obra técnica de nível médio. A Matemática é fundamental a esses profissionais por trabalhar competências relacionadas ao raciocínio lógico, ao poder de argumentação, à resolução de problemas, dentre outras. O artigo apresenta os resultados de uma pesquisa de caráter qualitativo que determinou, segundo quatro grupos de entrevistados, as demandas matemáticas necessárias aos técnicos de nível médio que atuam no setor upstream da indústria petrolífera da Bacia de Campos. Os resultados mostram conteúdos, metodologias e competências que interseccionam a Matemática no trabalho em diversos setores dessa indústria.
Palavras-chave: Região Norte Fluminense, Indústria petrolífera, Matemática.
Abstract: In the northern region of the Rio de Janeiro State, the oil industry is a strong employer of skilled technicians at High School level. Mathematics is crucial for these professionals because they work with skills including logical thinking, the power of reasoning and problem solving, among others. The article presents the results of a qualitative research survey that determined, according to four surveyed groups, which mathematical demands are necessary for the High School technicians that work in the upstream area of the oil industry in the Campos Basin. The results show that content, methodologies and skills intersect Mathematics and this type of work in various sectors of the industry.
Keywords: Northern Region of Rio de Janeiro, Oil industry, Mathematics.
1 Introdução
A indústria petrolífera emprega, desde a década de 1970, um grande número de trabalhadores da região Norte Fluminense (NF). A Bacia de Campos1, responsável por aproximadamente 80% da produção nacional de petróleo, está em uma nova fase com a descoberta da camada do pré-sal, num momento em que já era necessário compensar o declínio da produção dos campos de petróleo até então existentes. A quantidade e a qualidade do óleo encontrado possibilitam ao Brasil se tornar um grande exportador desse insumo bem como de seus derivados.
Com esse aumento na capacidade produtiva da atividade petrolífera, o NF passa a demandar profissionais de vários níveis, incluindo os técnicos de nível médio2, que irão atuar em empresas nacionais e multinacionais, operadoras e fornecedoras de bens e serviços.
Nesse contexto, a qualidade da Educação Básica é imprescindível para a garantia de empregabilidade de técnicos e de engenheiros brasileiros, em especial, os dessa região.
Dos nove municípios que compõem o NF, apenas um possui o Índice de Desenvolvimento da Educação Básica (Ideb) 2013 acima do nacional (Gráfico 1), considerando a nota obtida pelas escolas públicas urbanas na última série dos anos finais do Ensino Fundamental (8.ª série/ 9.º ano).
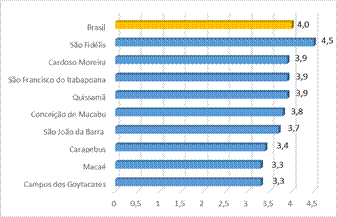
Gráfico 1 –
Ideb 2013 dos municípios da região Norte Fluminense
Fonte: BRASIL, 2014. Elaboração própria.
O Ideb varia de zero a dez e é calculado com base no desempenho dos alunos na Prova Brasil/Saeb e nas taxas de aprovação aferidas segundo as informações do Censo Escolar. A Prova Brasil avalia os estudantes em Língua Portuguesa e em Matemática (BRASIL, 2014).
Para a indústria petrolífera, esses conhecimentos são importantes no trabalho dos técnicos de nível médio. Elaboração de relatórios, leitura de mapas, cálculos de áreas dentre outros temas fazem parte da rotina desses trabalhadores.
Além disso, o contato com a Educação Tecnológica e com os conhecimentos da Física, imprescindível nessa área, a capacidade de raciocínio, de resolver problemas, de produzir argumentos, de prever e de interpretar resultados além do pensamento crítico estão diretamente relacionados às exigências desse mercado.
Em especial, a falta de conhecimento em Matemática vem atingindo não só os cursos técnicos mas também os de engenharia, que têm sua oferta aumentada a cada ano, na região NF e em todo o país. Em várias universidades, são criados laboratórios e disciplinas extracurriculares que revisitam conceitos matemáticos, básicos para os futuros engenheiros.
Uma ação da Coordenação de Ensino Médio do Instituto Federal de Educação, Ciência e Tecnologia Fluminense (IFFluminense) campus Campos Centro, feita em 2014, mostrou a frágil formação em Matemática de alunos que terminaram o Ensino Fundamental e que foram aprovados no processo seletivo para o curso técnico integrado ao Ensino Médio na modalidade regular.
Aplicou-se, para esses alunos, um pré-teste com questões de Matemática que abordavam os seguintes temas: operações com frações, unidades de medida, potenciação, radiciação, notação científica, área de polígonos, produtos notáveis, equação do primeiro e segundo graus, regra de três e teorema de Tales. O objetivo foi verificar as dificuldades dos alunos em Matemática e direcionar o trabalho dos professores dessa disciplina no sentido de sanar as dúvidas observadas. Numa etapa posterior, foram realizadas oficinas com os alunos que não conseguiram obter um mínimo de 70% de aproveitamento em cada um dos tópicos matemáticos apresentados no pré-teste.
O resultado é preocupante visto que 97% dos alunos tiveram que frequentar esses encontros para tentar recuperar os estudos. É importante lembrar que esses estudantes passaram por um processo seletivo bastante disputado e correspondem a uma amostra já “filtrada”, tanto da rede pública como da particular de várias cidades da região NF. A Tabela 1 traz o quantitativo dessa ação.
| Curso | Número de alunos que fizeram o pré-teste | Número de alunos com aproveitamento igual ou superior a 70% |
| Automação Industrial | 25 | 1 |
| Edificações | 54 | 1 |
| Eletrotécnica | 40 | 2 |
| Informática | 24 | 0 |
| Mecânica | 46 | 1 |
Em pauta, a qualidade da Educação Básica que compromete a formação de jovens da região e que colabora para importação de mão de obra, trabalhadores da indústria petrolífera e de outros grandes investimentos.
Num cenário mais amplo, os resultados do Indicador Nacional de Alfabetismo Funcional 2011 mostram que 57% das pessoas com Ensino Médio no país estão no nível básico de alfabetismo, cujas habilidades não contemplam a leitura de textos mais longos, a comparação e a avaliação de informações e a resolução de problemas envolvendo percentuais, proporções, além da interpretação de tabelas de dupla entrada, mapas, gráficos e imagens (INSTITUTO PAULO MONTENEGRO, 2012).
Na prática, o ensino de Matemática, e por que não dizer de outras ciências, é atingido pela falta de políticas públicas educacionais efetivas e de formação profissional qualificada, a interpretação equivocada de concepções pedagógicas, os erros conceituais presentes nos livros didáticos e o tratamento indevido aplicado aos conteúdos matemáticos como práticas manipulativas e aplicações artificiais (ONUCHIC, 1999; LIMA, 2002).
Esse artigo apresenta os resultados de uma pesquisa3que determinou, segundo os grupos entrevistados, as demandas matemáticas necessárias aos técnicos de nível médio que atuam no setor upstream4 da indústria petrolífera da Bacia de Campos.
O texto está estruturado em três seções. A primeira apresenta a fundamentação teórica que tem como base os Parâmetros Curriculares Nacionais do Ensino Médio - PCNEM (BRASIL, 2000). Na segunda seção, são apresentados os aspectos metodológicos da pesquisa e na terceira, os resultados referentes: (i) aos conteúdos matemáticos necessários ao trabalho dos técnicos da indústria petrolífera, (ii) às abordagens indicadas para a sala de aula, (iii) às competências e habilidades matemáticas exigidas pela indústria petrolífera no trabalho dos técnicos, (iv) à qualificação dos técnicos, (v) aos programas de capacitação; e (vi) às demandas da indústria petrolífera. Na quarta seção são expostos dois estudos relacionados ao tema e finalizando o artigo, as considerações finais.
2 Fundamentação teórica
A Lei de Diretrizes e Bases da Educação Nacional (LDB), de 20 de dezembro de 1996, declara no primeiro artigo: “A educação escolar deverá vincular-se ao mundo do trabalho e à prática social” (BRASIL, 1996, p.1). Nessa relação entre educação e trabalho, acredita-se que a formação dos técnicos de nível médio não pode prescindir da qualidade de ensino na Educação Básica, especialmente da sua última etapa, o Ensino Médio, que faz interface com o mundo produtivo.
Os PCNEM inspirados nos princípios da LDB/96 propõem uma reformulação para esse nível de ensino com um currículo voltado para competências e para as grandes áreas do conhecimento (BRASIL, 2000).
Segundo Perrenoud (2013, p.45): “[...] a competência é o poder de agir com eficácia em uma situação, mobilizando e combinando, em tempo real e de modo pertinente, os recursos intelectuais e emocionais”. O autor complementa afirmando que, de certo modo, a competência é uma promessa de desempenho, pois depende de fatores como o apoio ou a resistência dos outros atores envolvidos bem como a disponibilidade de ferramentas ou de tecnologias de qualidade (PERRENOUD, 2013).
Esse conceito se aproxima do de competência profissional, expresso nas Diretrizes Curriculares Nacionais para o Ensino Profissional de Nível Técnico (BRASIL, 1999a, p.24): “[...] capacidade de articular, mobilizar e colocar em ação valores, conhecimentos e habilidades necessários para o desempenho eficiente e eficaz de atividades requeridas pela natureza do trabalho”.
Os Parâmetros Curriculares Nacionais + do Ensino Médio (PCN+EM) apontam três competências gerais para as três áreas: (i) Ciências da Natureza, Matemática e suas Tecnologias; (ii) Ciências Humanas e suas Tecnologias; e (iii) Linguagens, Códigos e suas Tecnologias. Na primeira, a de comunicar e representar, articula-se a linguagem com seus símbolos e códigos, muitos já incorporados ao cotidiano, em diagramas, gráficos, esquemas e equações permitindo análises e sistematizações importantes em diversas atividades. Na segunda, a de investigar e compreender, valoriza-se a construção de modelos representativos e explicativos para a compreensão de leis naturais e de sínteses teóricas. Na terceira, a de contextualizar social ou historicamente os conhecimentos, é considerado o contexto em que se aplicam os conhecimentos científicos e tecnológicos e o caráter histórico da construção dos conhecimentos da área. Mesmo sendo admitidas especificidades quanto à Física, à Química, à Biologia e à Matemática, busca-se uma visão holística da história das ciências, numa visão ampliada sobre a cultura, a política e a economia (BRASIL, 2002).
Quanto às finalidades do Ensino Médio, apresentam-se: (i) a consolidação e o aprofundamento dos conhecimentos adquiridos no Ensino Fundamental; (ii) a preparação básica para o trabalho e a cidadania do educando; (iii) o desenvolvimento da autonomia intelectual e do pensamento crítico e (iv) a compreensão dos fundamentos científico-tecnológicos dos processos produtivos (BRASIL, 1996).
Em especial, nesse nível, o ensino de Matemática tem, dentre suas finalidades, que levar o aluno a:
[...] aplicar seus conhecimentos matemáticos a situações diversas, utilizando-os na interpretação da ciência, na atividade tecnológica e nas atividades cotidianas; analisar e valorizar informações provenientes de diferentes fontes, utilizando ferramentas matemáticas para formar uma opinião própria que lhe permita expressar-se criticamente sobre problemas da Matemática, das outras áreas do conhecimento e da atualidade; desenvolver as capacidades de raciocínio e resolução de problemas, de comunicação, bem como o espírito crítico e criativo; utilizar com confiança procedimentos de resolução de problemas para desenvolver a compreensão dos conceitos matemáticos; expressar-se oral, escrita e graficamente em situações matemáticas e valorizar a precisão da linguagem e as demonstrações em Matemática; estabelecer conexões entre diferentes temas matemáticos e entre esses temas e o conhecimento de outras áreas do currículo [...] (BRASIL, 2000, p.42).
O conhecimento matemático está presente nas ciências, na vida comum do cidadão e na estrutura mental que cada um desenvolve para se articular com seu meio. Por seu caráter universal, a linguagem dos números ultrapassa as suas finalidades mais imediatas e constrói, no ser humano, uma rica rede de habilidades ligadas a abstrações, modelos e argumentações. Embora o desenvolvimento dessas questões não aconteça apenas nas aulas de Matemática, a estrutura de organização dessa ciência ajuda o estudante na compreensão lógica dos fatos, na argumentação e na generalização de ideias.
A Matemática é considerada por D’Ambrosio (1996, p.7) como uma
estratégia desenvolvida pela espécie humana ao longo de sua história para explicar, para entender, para manejar e conviver com a realidade sensível, perceptível e, com o seu imaginário, naturalmente dentro de um contexto natural e cultural.
Para Lima (2002), essa ciência pode ser vista como arte, devido às conexões entre suas teorias, à elegância e à clareza dos seus raciocínios e à surpresa de algumas de suas conclusões. Serve também como linguagem operacional com seus símbolos numéricos e abstratos e como instrumento, pelas aplicações cotidianas ou ligadas a problemas tecnológicos e ao desenvolvimento de teorias científicas.
O papel instrumental também é destacado nos PCNEM. Segundo essa função, a Matemática deve ser considerada como um conjunto de técnicas e de estratégias a serem aplicadas em outras áreas do conhecimento, uma linguagem que permite modelar e interpretar a realidade: os números e a álgebra como sistema de códigos, a geometria na leitura e interpretação do espaço e a estatística na compreensão de fenômenos (BRASIL, 2000).
Outros dois papéis são considerados nos PCNEM: o estrutural, intrínseco à própria ciência, e o formativo. Quanto a esse último, contribui para formar no aluno a capacidade de resolver problemas, de adquirir hábitos de investigação e de análise, de enfrentar novas situações e desenvolver a criatividade, enfim, processos que irão ajudá-lo a estruturar o pensamento e o raciocínio dedutivo (BRASIL, 2000).
A formação escolar também não pode prescindir do uso de tecnologias, principalmente num mundo que vive a velocidade e os desafios de uma realidade sempre mutável. Deve contemplar os dois percursos: a Matemática para compreender a tecnologia e a tecnologia auxiliando o pensar matemático. Nesse último caso, apresentam-se os programas de geometria dinâmica que desenvolvem a visualização espacial, permitem o exercício da reflexão e da investigação, dentre outras habilidades. Planilhas eletrônicas também favorecem um trabalho com análise de dados e construções gráficas (BRASIL, 2000, 2006).
É importante ainda observar que a Matemática está, de forma direta ou indireta, presente nas competências profissionais de um técnico da área de indústria. Em destaque,
[...] elaborar planilha de custos de fabricação e de manutenção de máquinas e equipamentos, considerando a relação custo e benefício; [...] projetar produto, ferramentas, máquinas e equipamentos, utilizando técnicas de desenho e de representação gráfica com seus fundamentos matemáticos e geométricos; [...] elaborar projetos, leiautes, diagramas e esquemas, correlacionando-os com as normas técnicas e com os princípios científicos e tecnológicos; aplicar técnicas de medição e ensaios visando a melhoria da qualidade de produtos e serviços da planta industrial; avaliar as características e propriedades dos materiais, insumos e elementos de máquinas, correlacionando-as com seus fundamentos matemáticos, físicos e químicos para a aplicação nos processos de controle de qualidade; [...] e projetar melhorias nos sistemas convencionais de produção, instalação e manutenção, propondo incorporação de novas tecnologias [...] (BRASIL, 1999b, p.18-19).
3 Aspectos metodológicos
A pesquisa que norteia este artigo foi realizada no período de setembro de 2013 a fevereiro de 2014 e contou com a participação de quatro grupos: trabalhadores da Petrobras, recrutadores, supervisores e técnicos de empresas prestadoras de bens e serviços, coordenadores e professores de escolas de formação técnica e instrutores de um centro de treinamento que atende trabalhadores da indústria petrolífera.
As áreas consideradas para os dois primeiros grupos entrevistados, especificadas no Quadro 1, foram definidas a partir do estudo “Oportunidades e Desafios da Agenda de Competitividade para Construção de uma Política Industrial na Área de Petróleo: Propostas para um Novo Ciclo de Desenvolvimento Industrial” (FERNÁNDEZ Y FERNÁNDEZ; MUSSO, 2011).
Para o primeiro grupo, foram utilizadas áreas das três etapas (exploração, desenvolvimento e produção) do setor upstream da cadeia offshore e para o segundo, o elo dos drivers que compreende os seguintes setores: Sísmica, Serviços de poços, Apoio logístico, EPC (Engineering, Procurement and Construction) e estaleiros e Instalações submarinas (Figura 1).
A escolha deste elo se deu por envolver empresas que fornecem produtos e serviços de elevado grau de complexidade e de sofisticação tecnológica, além de manterem uma ligação mais direta com o operador ou petroleira. Selecionou-se, neste caso, no mínimo uma empresa para cada um dos setores citados.
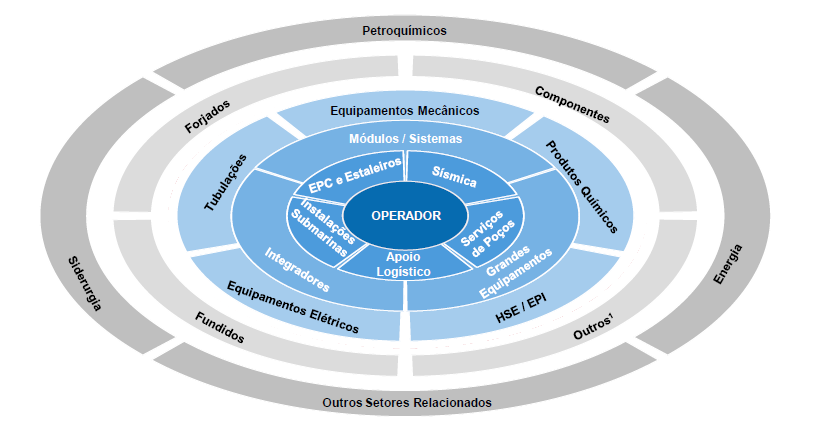
Figura 1 -
Caracterização da cadeia de fornecimento de bens e serviços offshore
Fonte: Fernández y Fernández e Musso, 2011, p.4.
A coleta de dados foi feita por meio de entrevistas semiestruturadas5 e de pesquisas documentais. Nesse último caso, estão as informações que complementaram as entrevistas como dados referentes às empresas entrevistadas, aos softwares utilizados em alguns setores e programas de capacitação. Quanto aos protocolos das entrevistas, os temas abordados foram: (i) as exigências no processo seletivo das empresas; (ii) os cursos que são ministrados aos técnicos no início da fase de trabalho; (iii) o perfil do técnico exigido pela indústria petrolífera; (iv) a formação em Matemática que se observa nos técnicos quando iniciam os trabalhos nessa indústria; (v) os conteúdos matemáticos necessários à área de atuação de cada técnico entrevistado; (vi) as competências e habilidades matemáticas que constam nos PCNEM e que são imprescindíveis ao técnico de nível médio na indústria petrolífera; e (vii) a relação entre a escola e o mercado de trabalho (ações conjuntas, dificuldades dos alunos em Matemática, propostas para a sala de aula). Neste artigo serão priorizados os três últimos temas.
De caráter qualitativo, a pesquisa investigou diversos setores da indústria petrolífera que utilizam a Matemática de forma diferenciada. Nesse tipo de pesquisa, prioriza-se o aprofundamento da compreensão de um grupo social ou de uma instituição sobre um determinado tema. Sendo assim, o número de pessoas envolvidas na pesquisa é menos importante do que a possibilidade de discutir uma questão sob várias perspectivas (GOLDENBERG, 2009).
O Quadro 1 traz o quantitativo dos grupos entrevistados e as especificações das áreas selecionadas.
| Quantidade | ENTREVISTADOS | Quantidade | ÁREAS |
| 10 | Trabalhadores da Petrobras | 1 | Construção de unidades de produção |
| 1 | Desenvolvimento da produção | ||
| 1 | Apoio logístico | ||
| 6 | Manutenção, modificação e operação de embarcação | ||
| 1 | Exploração e Avaliação | ||
| 20 | Recrutadores, supervisores e técnicos das fornecedoras de bens e serviços | 2 | Sísmica |
| 2 | EPC e estaleiros | ||
| 2 | Instalações submarinas | ||
| 3 | Apoio logístico | ||
| 11 | Serviços de poços | ||
| 6 | Coordenadores e professores de cursos relacionados à indústria de petróleo e gás* | ||
| 2 | Instrutores de um centro de treinamento | ||
A seguir, são apresentados os resultados da pesquisa considerando a metodologia exposta nesta seção.
4 Resultados da pesquisa
4.1 Conteúdos matemáticos
Os temas mais citados pelos entrevistados foram: operações numéricas, grandezas e medidas, proporcionalidade, função afim, trigonometria, geometria plana, espacial e analítica e leitura de gráficos e de mapas. Outros, como desenho geométrico, lógica booliana e cálculo diferencial foram considerados por trabalhadores de áreas mais específicas. Um entrevistado citou ainda a necessidade de o técnico ter um conhecimento mínimo sobre Matemática financeira, pois, em reuniões, temas como lucro, receita e custo são tratados rotineiramente.
As operações numéricas estão presentes em diversas ações e envolvem cálculos com potências de 10, principalmente na conversão de unidades. O técnico precisa operar números com uma ordem de grandeza elevada assim como operá-los nas formas decimal e fracionária. A linguagem percentual também deve ser de domínio desse profissional, pois aparece em gráficos, planilhas e em informações fornecidas frequentemente.
Alguns entrevistados citaram o uso excessivo da calculadora para cobrir um deficitem operações básicas. Em alguns casos, os técnicos não percebem resultados absurdos gerados por uma falha de digitação. A falta de conhecimento sobre ordens e classes de um número também foi observada gerando leituras do tipo “dez quarenta” para 1.040 ou “um quatro cinco dois sete oito e nove” para 1.452.789.
As unidades de medida também aparecem com frequência, principalmente numa atividade em que os conceitos físicos são fundamentais como os de mecânica, elétrica, termodinâmica, hidráulica, pneumática, dentre outras áreas. Apesar de o Sistema Internacional (SI) ser adotado por muitos países, ainda são comuns equipamentos, livros e manuais que utilizam outros sistemas, como o inglês e o americano, criando a necessidade de fatores de conversão (Quadro 2).
| Grandeza | Unidade inglesas ou americanas | Sistema Internacional (SI) | Fator de conversão |
| comprimento | polegada (in) | milímetro (mm) | 1 in = 25,4 mm |
| pé (ft) | metro (m) | 1 ft = 0,3048 m | |
| área | polegada quadrada (in2) | centímetro quadrado (cm2) | 1 in2 = 6,452 cm2 |
| pé quadrado (ft2) | metro quadrado (m2) | 1 ft2 = 0,09290 m2 | |
| Volume* | polegada cúbica (in3) | centímetro cúbico (cm3) | 1 in3=16,39 cm3 |
| pé cúbico (ft3) | metro cúbico (m3) | 1 ft3 = 0,02832 m3 | |
| galão americano (gal) | decímetro cúbico** (dm3) | 1 gal = 3,789 dm3 ou 3,789 L | |
| barril de petróleo americano (bbl) | decímetro cúbico (dm3) | 1 bbl= 158,987 dm3 ou 158,987 L | |
| densidade | libra por pé cúbico (lbm/ft3) | quilograma por metro cúbico (kg/m3) | 1 lbm/ft3 = 16.02 kg/m3 |
| torque | libra-força-pé (lbf.ft) | newton-metro (N.m) | 1 lbf.ft = 1,356 N.m |
| pressão | libra por polegada quadrada (psi) | newton por metro quadrado (Pa) | 1 psi = 6895 Pa |
| libra por pé quadrado (psf) | 1 psf = 47,88 Pa | ||
| bar | 1 bar = 105Pa | ||
| frequência | ciclo por segundo (cps) | hertz (Hz) | 1 cps = 1,0 Hz |
| vazão volumétrica | pé cúbico por minuto(ft3/min) | metro cúbico por segundo (m3/s) | 1ft3 /min = 4,719 x 10-4m3/s |
| galão por minuto (gpm) | metro cúbico por segundo (m3/s) | 1 gpm = 6,309 x 10-5 m3/s | |
| Barril por dia (bpd) | metro cúbico por segundo (m3/s) | 1 bpd = 1,840 131 x 10-6 m3/s |
Num universo de tanta tecnologia, não é necessário que o técnico decore os fatores de conversão, pois as planilhas eletrônicas dão conta dessa função; porém o conhecimento das unidades, a comparação entre elas e a noção de tamanho são fundamentais para se tomar decisões e agir rapidamente quando necessário. Plataformas da Petrobras trabalham com unidades diferentes das de outros fornecedores internacionais. Assim, o técnico tem que estar habituado a fazer as conversões já que essa prática faz parte da rotina de trabalho.
O conceito de proporcionalidade, implícito nessas conversões, também aparece nas fórmulas matemáticas, gráficos e experimentos. Grandezas diretamente ou inversamente proporcionais estão presentes em conceitos como os de densidade (diretamente proporcional à massa e inversamente proporcional ao volume) e de pressão hidrostática (diretamente proporcional à profundidade e à densidade do líquido).
Alguns entrevistados alertaram para o uso indiscriminado da regra de três tornando mecânica a solução de algumas questões simples bem como a dificuldade em entender o conceito de escala que prejudica a confecção e a leitura de mapas e de gráficos.
Em relação às funções, apenas a função afim ganhou destaque, associada a assuntos como pressão hidrostática exercida por fluidos, potência e força elástica. Na trigonometria, as respostas foram direcionadas às aplicações que envolvem o seno, o cosseno e a tangente no triângulo retângulo. Apenas um entrevistado citou o estudo das funções trigonométricas, das transformações gráficas, das identidades e das equações.
Na geometria, foram muitas as aplicações. Na plana, a área de figuras ajuda o técnico em situações que vão do uso do princípio de Pascal para vasos comunicantes em que o conhecimento da área do círculo sobre a qual será exercida uma força é fundamental, até o orçamento de pintura de uma plataforma. O comprimento da circunferência e o teorema de Pitágoras também são necessários em diversas situações. Esse último, na resultante de forças, no cálculo de distâncias, entre outros.
Na geometria espacial, o volume de sólidos, especialmente o paralelepípedo, o cilindro e a esfera merecem destaque. O formato dos tanques impõe tal ênfase uma vez que os de suprimento, onde são colocados produtos químicos, podem apresentar o formato de um paralelepípedo, os de armazenamento são cilíndricos ou esféricos e os separadores bifásicos (líquido e gás) e trifásicos (óleo, água e gás) possuem um formato cilíndrico com semiesferas nas extremidades.
O cilindro se sobressai, pois além dos tanques, uma grande parte das bombas, da tubulação e das ferramentas têm esse formato. Vale ressaltar que, no processo de desativação e de abandono das atividades de produção, é preciso que se faça o cálculo do volume das tubulações cilíndricas que ligam os equipamentos, que estão no fundo do mar, até as plataformas. Nos tanques, o cálculo correto do volume garante segurança à unidade marítima, prevenindo-a de adernar.
Em geometria analítica, foi destacado o estudo de vetores, fundamental para a compreensão do cálculo estrutural e de assuntos da Física como sistema de forças em plano inclinado e com roldanas. Também foi relatada a importância de se conhecer outros sistemas de coordenadas, além do plano e do espaço cartesianos, estudados em sala de aula. Outros três foram citados: o de coordenadas UTM (Universal Transversa de Mercator), geográficas e polares.
O sistema de coordenadas UTM mede distâncias e é o mais utilizado no Brasil, na confecção de mapas de projeções. A correlação entre o plano cartesiano e o sistema de coordenadas UTM é simples: o eixo y se associa ao eixo N (Northing) que representa a medida norte/sul e o eixo x ao eixo E (Easting), representando a medida leste/oeste. Qualquer posição de um objeto em coordenadas UTM se descreve por meio de três elementos: a zona6 em que está, o easting e o northing (ROCHA et al., 2011).
O sistema de coordenadas geográficas indica a latitude e a longitude de um ponto na superfície terrestre, e o de coordenadas polares indica a medida linear referente à distância e a angular referente à direção. Em entrevista, foi citada uma situação em que o uso das coordenadas polares determinava a posição de uma boia situada a 700 metros da âncora do navio e posicionada sob uma determinada direção desta.
Nas entrevistas, o tópico mais citado foi a leitura de gráficos e de mapas que exige precisão na interpretação de dados. Os gráficos são utilizados para diferentes finalidades como o conhecimento sobre o perfil de um poço feito por meio da análise de inúmeras grandezas: porosidade, resistividade, densidade, dentre outras. A presença de jazidas comerciais de petróleo é confirmada a partir da interpretação desses perfis.
O monitoramento do comportamento de grandezas, como pressão, temperatura, vazão, densidade e velocidade, também é feito por imagens gráficas contidas em equipamentos de alto teor tecnológico. Existem algumas funções técnicas que só cuidam desse monitoramento e interferem no processo quando ocorre um problema. São situações que exigem velocidade de raciocínio e competência técnica para encontrar soluções. É importante destacar que o controle das três primeiras é fundamental para os que cuidam das unidades de desenvolvimento e de tratamento de óleo e gás.
Quanto às cartas topográficas, a leitura envolve conhecimentos sobre escala, sistemas de coordenadas, curvas de nível, dentre outros.
Em alguns assuntos, como desenho geométrico, foram lembradas as dificuldades de alguns técnicos no manuseio de instrumentos geométricos como compasso, transferidor e esquadro.
O cálculo diferencial e a lógica booliana não ficaram de fora dessa seleção devido às aplicações no cálculo estrutural e na compreensão de circuitos elétricos, respectivamente.
Dentre os conteúdos citados nas entrevistas, alguns não são estudados na Educação Básica, como coordenadas polares e cálculo diferencial. Outros merecem uma revisão na abordagem, como a trigonometria; quando vista em sua totalidade no Ensino Médio, é longa, abstrata e carece de exemplos práticos.
Segundo os PCNEM, deve-se evitar, no estudo da trigonometria, o número excessivo de cálculos algébricos em equações e identidades. O que precisa ser assegurado são as aplicações na resolução de problemas que envolvem medições, em especial no cálculo de distâncias inacessíveis, e na construção de modelos que representam fenômenos periódicos (BRASIL, 2000). Lima (2001), em sua análise de livros de Matemática para o Ensino Médio, corrobora essa opinião. Afirma ser esse um estudo com ênfase em trivialidades e ausência de problemas contextuais atraentes, além de conceitos mal definidos como o radiano e do pouco uso de calculadoras.
Esse mesmo autor comenta sobre a oportunidade desperdiçada de rever o conceito de proporcionalidade no estudo da função afim e da interpretação vetorial praticamente omitida no estudo da geometria analítica (LIMA, 2001).
Durante as entrevistas, os profissionais das instituições de ensino e do centro de treinamento afirmaram que, nos cursos ministrados, a cada ano se percebe uma maior defasagem em relação aos conceitos de Matemática básica. Em cursos abertos à comunidade, essa deficiência é ainda maior por contar com alunos advindos de cursos técnicos com baixa qualificação. Além disso, as fornecedoras, que muitas vezes financiam esses cursos, contratam os alunos com maior rendimento, ficando cada vez mais difícil a inserção de jovens, que possuem fragilidades em sua formação básica, no mercado de trabalho.
4.2 Abordagens para a sala de aula
Os entrevistados citaram abordagens que deveriam ser praticadas nas aulas de Matemática e que ajudariam o técnico a adquirir atitudes positivas frente ao trabalho na indústria petrolífera.
A valorização do raciocínio, do cálculo mental e da estimativa foi apontada como fundamental nesse tipo de ocupação. Embora o uso de calculadoras e de softwares seja bem explorado, muitas vezes é exigido do técnico rapidez de raciocínio frente a novas situações ou mesmo em reuniões. Estimativa de custos, de tempo, de ocupação de cargas em galpões, de produção diária de petróleo e sobre a resistência de materiais são feitas com frequência. Muitas vezes, o cálculo envolve números elevados exigindo algoritmos mentais bem sofisticados.
Outro aspecto importante é a apresentação de situações-problema em vez de questões do tipo “Calcule”. Nesse tipo de trabalho, resolvem-se problemas todo o tempo e vivenciam-se questões passíveis a mudanças e a adaptações. Alguns entrevistados disseram que, mesmo em um ambiente automatizado, ocorrem erros e problemas com os equipamentos. Nesses casos, muitas variáveis devem ser consideradas na busca por uma solução. Valoriza-se, então, a aplicação de problemas contextualizados em que o técnico possa enfrentar situações novas, sendo capaz de modelá-las matematicamente. De acordo com os PCN+EM, exercícios do tipo “Calcule...” não devem ser eliminados, pois cumprem a função do aprendizado de técnicas e propriedades, porém não oferecem aos alunos uma visão de mundo abrangente (BRASIL, 2002).
Segundo os PCNEM, a resolução de problemas favorece a contextualização, desenvolve a capacidade de raciocínio e amplia a autonomia e a capacidade de comunicação e de argumentação dos estudantes. Em confronto com situações-problema novas, os alunos planejam etapas, estabelecem relações, verificam regularidades e fazem uso dos erros anteriores para buscar novas alternativas (BRASIL, 2000). É válido ressaltar que não se trata de exercícios de aplicação de técnicas matemáticas em que várias questões com passos análogos são resolvidas. É preciso desafiar o aluno com situações diferentes ou mais complexas (BRASIL, 2002).
Também foi destacada a importância nesse tipo de atividade com as tecnologias. De planilhas como o Excel utilizadas com frequência pelo apoio logístico no controle de custos, de embarque e desembarque de pessoal, a softwares mais específicos como os que monitoram o posicionamento de unidades marítimas, o técnico deverá, além de inserir dados, saber ler, interpretar informações e identificar possíveis inadequações ou erros. Também está sendo avaliada a sua capacidade de flexibilização uma vez que as atualizações e as trocas de programas são feitas constantemente.
O uso de tecnologias no ensino da Matemática reforça a importância da linguagem gráfica e de novas formas de representação além de relativizar o papel do cálculo e da manipulação simbólica. O trabalho com o computador na sala de aula permite o aluno investigar e buscar estratégias para a solução de problemas, respeitando o seu ritmo de aprendizagem e levando em considerações os seus erros (BRASIL, 1998).
4.3 Competências e Habilidades
Foi solicitado aos entrevistados que indicassem, dentre as competências matemáticas apontadas pelo PCNEM, aquelas que eram imprescindíveis ao técnico de nível médio. Optou-se por trabalhar com os PCNEM por entender que essa última etapa da Educação Básica, na interface com o mundo produtivo, contribui de forma decisiva para consolidar outras competências e habilidades adquiridas no Ensino Fundamental.
Percebeu-se a importância da leitura de gráficos, da contextualização dos assuntos matemáticos e do uso apropriado de tecnologias nesse tipo de atividade. O Gráfico 2 expõe os resultados

Gráfico 2 -
Competências e habilidades matemáticas indicadas nos PCNEM importantes à atuação do técnico de nível médio na indústria petrolífera
Fonte: Elaboração própria.
4.4 A qualificação dos técnicos, os programas de capacitação e as demandas do mercado
A entrevista semiestruturada, utilizada na metodologia da pesquisa, possibilitou o levantamento de questões que agregaram valor à pesquisa.
Os trabalhadores da Petrobras e das empresas fornecedoras chamaram a atenção para os técnicos recém-formados que, segundo eles, chegam ao mercado de trabalho cada vez mais despreparados. Imaturidade emocional, questões comportamentais e erros técnicos têm justificado o uso da automação, mesmo em setores em que seria mais rentável o trabalho humano.
Além disso, estão limitados na tomada de decisões. Agem robotizados, sem capacidade analítica nem bom-senso. Cabe lembrar que o conceito de competência profissional demanda a mobilização de valores, de conhecimentos e de habilidades para além dos problemas rotineiros. Espera-se que o técnico atue de forma eficaz diante do inesperado explorando sua criatividade (BRASIL, 1999a).
Apresentam cada vez mais certificações, porém estão menos qualificados. Uma das recrutadoras de uma empresa fornecedora disse que um dos candidatos não conseguiu falar em 10 minutos sobre os assuntos mais relevantes de um curso que acabara de fazer, de 10 meses de duração. Pastore (2006) afirma que para um jovem se inserir no mercado de trabalho é preciso ter respostas, não necessariamente diploma. A empregabilidade, segundo Pastore, depende da boa educação: bom-senso, lógica de raciocínio, criatividade, autonomia, capacidade de trabalhar em grupo e de educar-se permanentemente, diferentemente do adestramento oferecido por muitas escolas.
Outros temas surgiram durante as entrevistas como os programas especiais de capacitação oferecidos por algumas empresas a recém-contratados. São programas de formação acelerada com investimentos em cursos teóricos e práticos, oferecidos aos jovens com bons currículos e que obtiveram melhor desempenho no processo seletivo da empresa.
Também é realidade para alguns alunos a entrada no mercado de trabalho sem a realização de provas para processo seletivo. O contrato é feito mediante as notas obtidas no Ensino Médio e no curso técnico. Após a contratação, o aluno é admitido como estagiário, recebe treinamento teórico e prático na empresa e sua permanência depende da dedicação quanto à rotina de estudos. Nessas situações, a importância da qualidade da Educação Básica irá garantir a entrada e a permanência dos jovens nesse mercado de trabalho.
Foi constatada também, durante as entrevistas, uma demanda por profissionais técnicos em Geologia, em Geomática, em Geodésia7, em Geoprocessamento e em Cartografia. Os profissionais que trabalham nessas áreas são oriundos, em maioria, de Minas Gerais e do Espírito Santo.
5 Estudos Relacionados
Nesta seção, são apresentadas duas pesquisas relacionadas ao tema deste artigo. Buscou-se uma intersecção pela utilização da Matemática no trabalho dos técnicos de nível médio que atuam no setor industrial.
A primeira é o trabalho de conclusão de curso de graduação intitulado A Matemática utilizada pelos técnicos em eletroeletrônica na indústria automobilística escrito por Erotide Rodrigues Pereira e orientado pela Profª. Drª. Elisabete Zardo Búrigo em 2013 na Universidade Federal do Rio Grande do Sul.
O objetivo do trabalho é verificar quais os conhecimentos matemáticos são utilizados pelos técnicos em eletroeletrônica no seu ambiente de trabalho. Foram entrevistados quatro técnicos que atuam no setor de manutenção em uma indústria do setor automobilístico da região metropolitana de Porto Alegre. A metodologia utilizada foi a entrevista semiestruturada e a observação, neste caso, da rotina dos técnicos nessa indústria.
Verificou-se, ao final da pesquisa, que a Matemática utilizada por esses técnicos envolve a álgebra, as operações de soma, subtração, multiplicação e divisão, o estudo e a representação gráfica das funções e o raciocínio lógico.
Os conhecimentos matemáticos nessa indústria são importantes para: (i) facilitar o entendimento, por meio da leitura dos manuais técnicos, da integração entre diversos equipamentos como: o Controlador Lógico Programável (CLP)8, o transformador e o controlador de solda; (ii) garantir a maior segurança na tomada de decisões; (iii) facilitar a proposição de melhorias no processo produtivo; (iv) permitir adaptações, quando necessárias, na lógica de programação do CLP; (v) permitir a detecção e correção de situações imprevisíveis existentes na programação de softwares da área de manutenção; e (vi) contribuir para o desenvolvimento de ferramentas gráficas para o monitoramento do tempo das operações, garantindo a otimização e o melhor acompanhamento do processo produtivo.
Pereira (2013) cita os Parâmetros Curriculares Nacionais (BRASIL, 1998) destacando a importância da Matemática na estruturação do pensamento, na agilização do raciocínio dedutivo do aluno e na aplicação a problemas do cotidiano e do trabalho. Ressalta a necessidade de uma formação escolar adequada na Educação Básica, requisito para uma formação técnica de qualidade.
Dessa forma, a autora reforça alguns resultados obtidos pela pesquisa apresentada neste artigo como a importância, para os técnicos de nível médio, do raciocínio lógico, num universo tecnológico em que o capital humano, apesar da crescente automação dos processos industriais, é imprescindível na tomada de decisões. Também é ponto comum entre os resultados apresentados nesses trabalhos a importância da leitura de gráficos, das operações matemáticas básicas e da flexibilização dos técnicos na compreensão de novos programas computacionais que surgem frequentemente.
A segunda pesquisa é a dissertação: Competências e habilidades matemáticas no trabalho de técnicos de nível médio e engenheiros do setor industrialde autoria de Cleiton Geraldo Mendes Miranda. Orientada pelo Prof. Dr. João Bosco Laudares em 2012, no Centro Federal de Educação Tecnológica de Belo Horizonte, tem como objetivo estudar as competências e habilidades matemáticas no trabalho de técnicos de nível médio e de engenheiros do setor industrial. Não são feitas análises em relação aos engenheiros devido ao escopo da pesquisa que norteia esse artigo.
Miranda (2012) utilizou a metodologia de pesquisa qualitativa e a coleta de dados foi feita por meio de entrevistas semiestruturadas com um roteiro estruturado em torno de sete categorias de análise, a saber: (i) a formação inicial do entrevistado; (ii) a escolha do curso de formação profissional; (iii) a Matemática no curso de formação profissional; (iv) o uso da Matemática no trabalho; (v) o uso de tecnologias; (vi) as estratégias de aprendizagem de Matemática; (vii) os conteúdos de Matemática no trabalho. Foram entrevistados técnicos de quatro empresas da região metropolitana de Belo Horizonte ligados às áreas de segurança do trabalho, informática, mecânica, telecomunicações e eletrotécnica.
Destacam-se os resultados de Miranda (2012) que corroboram os apresentados neste artigo:
-
a necessidade de uma boa “base” em Matemática, pois é um dos motivos da elevada taxa de evasão nos cursos de formação profissional além de desabilitar os técnicos de nível médio à entrada nas empresas;
-
a importância para as atividades laborais dos técnicos de estudos que envolvam: operações de multiplicação e divisão, regra de três, trigonometria, porcentagem, construção e análise gráfica;
-
o uso de ferramentas computacionais como softwares de simulação, de desenho e de programação. Foram citados como sendo de uso frequente as calculadoras científicas, o AutoCAD e o Excel;
-
a conveniência na utilização do cálculo exato e do aproximado. O aproximado indicado em visitas de campo, nas operações de custo, de prazo e de estimativa e o exato no momento da execução e fabricação do produto;
-
a falta de ligação entre os conteúdos de Matemática estudados na escola e as outras disciplinas do curso de formação profissional assim como as demandas do mercado de trabalho; e
-
a importância da contextualização dos conteúdos, considerada fator de motivação na aprendizagem da Matemática.
A dissertação apresenta ainda as estratégias matemáticas mais utilizadas pelos técnicos de nível médio, dentre as opções apresentadas pelos pesquisados nas entrevistas: análise de dados, estatística, resolução de problemas, modelagem matemática, cálculo operacional e conceitos matemáticos. Os resultados são apresentados no Gráfico 3:
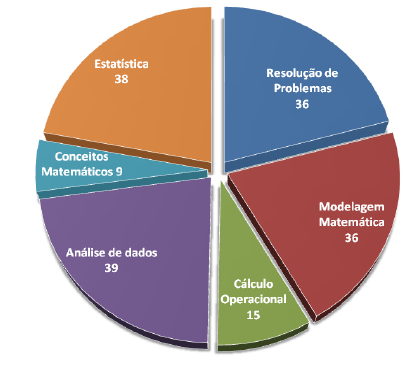
Gráfico 3 -
Estratégias matemáticas mais utilizadas no trabalho por técnicos de nível médio
Fonte: MIRANDA, 2012, p. 1119.
As entrevistas realizadas por Pereira (2013) e Miranda (2012) mostram que o conhecimento matemático é uma ferramenta valiosa no trabalho desenvolvido pelos técnicos de nível médio no setor industrial.
6 Considerações finais
A nova fronteira de produção da Bacia de Campos só poderá se transformar em alavanca para o desenvolvimento regional se nela se agregar um conjunto de ações em direção à formação dos jovens da região. A busca por uma Educação Básica de qualidade afasta a possibilidade da importação de mão de obra.
Políticas Públicas vêm sendo implementadas em todo o país de modo a otimizar o acesso desses jovens ao mercado de petróleo e gás. Muitos não têm conseguido aproveitar as oportunidades de emprego, oferecidas pela atividade petrolífera, em parte pela falta de escolaridade. Em um mercado de poucas vagas, a porta de entrada tem sido aberta aos que trazem conhecimento, capacidade em inovação e domínio de tecnologias em seu portfólio.
Os resultados apresentados revelam conteúdos, metodologias e competências matemáticas importantes nesse mercado. Percebem-se carências no cálculo com operações básicas e uma atitude passiva dos técnicos frente aos problemas que surgem no trabalho. Há a indicação de um estudo em sala de aula que valorize o cálculo mental, a resolução de problemas, a estimativa, o raciocínio lógico e o uso de tecnologias.
São questões importantes não só para os técnicos mas para alunos e professores da Educação Básica e do Ensino Superior, em especial os que atuam nas Engenharias e nas Licenciaturas em Matemática e áreas afins. Convém lembrar que a LDB (BRASIL, 1996), em seu artigo 26, indica para a parte diversificada dos currículos do Ensino Fundamental e Médio, conteúdos exigidos segundo as características e as economias regionais.
Nos estudos relacionados, outros locais do país, representados por Belo Horizonte e Porto Alegre, tiveram trabalhos semelhantes que corroboram os resultados apresentados neste artigo. A importância de se oferecer uma Educação Básica de qualidade que alicerce o trabalho de futuros técnicos é ponto comum entre as pesquisas apresentadas.
O tema deste artigo é de extrema relevância para a região NF, pois contribui para a qualificação da mão de obra voltada à indústria do petróleo, forte empregadora dessa região. Embora estejam voltados para a Bacia de Campos, os resultados obtidos podem se aplicar a outros locais de produção, pois a caracterização da cadeia de fornecimento de bens e serviços e das atividades e processos realizados pelas petroleiras é válida em todo o território nacional.
Referências
BRASIL. Conselho Nacional de Educação. Parecer nº. 16, de 5 de outubro de 1999. Trata das diretrizes curriculares nacionais para a educação profissional de nível técnico. Diário Oficial [da] República Federativa do Brasil, Brasília, DF, 26 nov. 1999a. Disponível em: http://portal.mec.gov.br/setec/arquivos/pdf_legislacao/tecnico/legisla_tecnico_parecer1699.pdf. Acesso em: 10 jul. 2014.
BRASIL. Resolução nº. 4, de 8 de novembro de 1999. Institui as diretrizes curriculares nacionais para a educação profissional de nível técnico. Diário Oficial [da] República Federativa do Brasil, Brasília, DF, 22 dez. 1999b. Disponível em: http://portal.mec.gov.br/setec/arquivos/pdf_legislacao/tecnico/legisla_tecnico_resol0499.pdf. Acesso em: 20 jun. 2014.
BRASIL. Ministério da Educação. Ideb. Brasília: Inep/MEC, 2014. Disponível em: http://ideb.inep.gov.br/. Acesso em: 10 set. 2014.
BRASIL. Ministério da Educação. Lei de Diretrizes e Bases nº. 9.394, de 20 de dezembro de 1996. Fixa as diretrizes e bases da educação nacional. Diário Oficial [da] República Federativa do Brasil, Brasília, DF, 23 dez. 1996. Disponível em: http://www.planalto.gov.br/ccivil_03/Leis/L9394.htm. Acesso em: 25 jul. 2013.
BRASIL. Ministério da Educação. Secretaria de Educação Básica. Orientações curriculares para o ensino médio: ciências da natureza, matemática e suas tecnologias. Brasília: MEC/ SEB, 2006.
BRASIL. Ministério da Educação. Secretaria de Educação Básica. Parâmetros Curriculares Nacionais do Ensino Médio. Brasília: MEC/SEB, 2000.
BRASIL. Ministério da Educação. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF, 1998.
BRASIL. Ministério da Educação. Secretaria de Educação Média e Tecnológica. Parâmetros Curriculares Nacionais + Ensino Médio: orientações educacionais complementares aos Parâmetros curriculares nacionais. Brasília: MEC/SEMTEC, 2002.
BRASIL. Ministério do Trabalho e Emprego. Classificação Brasileira de Ocupações. 3.ed. Brasília: MTE/SPPE, 2010. v. 3
BUREAU INTERNATIONAL DES POIDS ET MESURES (BIPM). NIST Guide to the SI. 2014. Disponível em: http://physics.nist.gov/Pubs/SP811/appenB9.html. Acesso em: 20 maio 2014.
CAETANO FILHO, Elisio. O papel da pesquisa nacional na exploração e explotação petrolífera da margem continental na Bacia de Campos. In: PIQUET, Rosélia (Org.). Petróleo, royalties e região. Rio de Janeiro: Garamond, 2010. p. 39-94.
D’AMBROSIO, Ubiratan. Educação Matemática: da teoria à prática. Campinas: Papirus, 1996. (Coleção Perspectivas em Educação Matemática).
FERNÁNDEZ Y FERNÁNDEZ, Eloi; MUSSO, Bruno. Oportunidades e Desafios da Agenda de Competitividade para Construção de uma Política Industrial na Área de Petróleo: Propostas para um Novo Ciclo de Desenvolvimento Industrial. In: FÓRUM NACIONAL, 23., 2011, Rio de Janeiro. Anais... Rio de Janeiro: INAE, 2011. p. 1-37.
GOLDENBERG, Mirian. A arte de pesquisar: como fazer uma pesquisa qualitativa em ciências sociais. Rio de Janeiro: Record, 2009.
INSTITUTO NACIONAL DE METROLOGIA, QUALIDADE E TECNOLOGIA (INMETRO). Sistema Internacional de Unidades SI. Duque de Caxias, RJ: INMETRO: CICMA: SEPIN, 2012.
INSTITUTO PAULO MONTENEGRO. Inaf Brasil 2011. São Paulo: Instituto Paulo Montenegro e Ação Educativa, 2012.
LIMA, Elon Lages. Exame de Textos: Análise de livros de Matemática para o Ensino Médio. Rio de Janeiro: VITAE: IMPA: SBM, 2001.
LIMA, Elon Lages. Matemática e Ensino. Rio de Janeiro: SBM, 2002. (Coleção do Professor de Matemática).
MIRANDA, Cleiton Geraldo Mendes. Competências e habilidades matemáticas no trabalho de técnicos de nível médio e de engenheiros do setor industrial. 2012. 132 f. Dissertação (Mestrado em Educação Tecnológica) – Centro Federal de Educação Tecnológica de Minas Gerais, Belo Horizonte, 2012.
MOREIRA, Herivelto; CALEFFE, Luiz Gonzaga. Metodologia da pesquisa para o professor pesquisador. 2.ed. Rio de Janeiro: Lamparina, 2008.
ONUCHIC, Lourdes de la Rosa. Ensino-aprendizagem de Matemática através da resolução de problemas. In: BICUDO, Maria Aparecida Viggiani (Org.). Pesquisa em Educação Matemática: concepções e perspectivas. São Paulo: Editora UNESP, 1999. p.199-218. (Seminários e Debates).
PASTORE, José. As mudanças no mundo do trabalho: leituras de sociologia do trabalho. São Paulo: LTr, 2006.
PEREIRA, Erotide Rodrigues. A Matemática utilizada pelos técnicos em eletroeletrônica na indústria automobilística. 2013. 105 f. Trabalho de Conclusão de Curso (Licenciatura em Matemática) – Universidade Federal do Rio Grande do Sul, Porto Alegre, 2013.
PERRENOUD, Philippe. Desenvolver Competências ou Ensinar Saberes? A escola que prepara para a vida. Tradução de Laura Solange Pereira. Porto Alegre: Penso, 2013.
PETROBRAS. Glossário. 2014. Disponível em: http://www.investidorpetrobras.com.br/pt/glossario/. Acesso em: 29 maio 2014.
POTTER, Merle; SCOTT, Elaine.Termodinâmica. Tradução de Alexandre Arcanjo, Helena Bononi e Suely Cuccio. São Paulo: Thomson Learning, 2006.
ROCHA, Luiz Alberto Santos et al. Perfuração Direcional. Rio de Janeiro: Interciência: Petrobras: IBP, 2011.
Notas
Notas de autor